1. Introduction
2. Thermo-elasto-plastic analysis
Table┬Ā1
| Case no. | Welding current (A) | Arc voltage (V) |
|---|---|---|
| 1 | 100 | 25 |
| 2 | 100 | 24 |
| 3 | 100 | 23 |
| 4 | 100 | 22 |
| 5 | 90 | 25 |
| 6 | 90 | 24 |
| 7 | 90 | 23 |
| 8 | 90 | 22 |
| 9 | 80 | 25 |
| 10 | 80 | 24 |
| 11 | 80 | 23 |
| 12 | 80 | 22 |
Table┬Ā1
| Parameter | Value |
|---|---|
| Convection | 22┬░C |
| Material condition | Titanium |
| Welding speed | 40 cm/min |
| Solver type | Transient thermal, static structural |
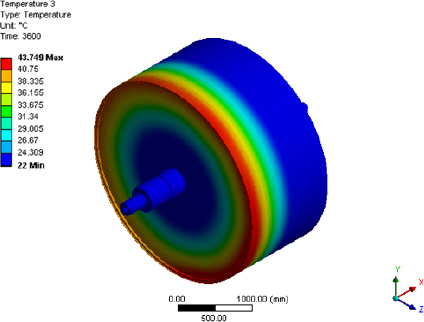
| Cooling time | 3,600 sec |
| Gravitational acceleration | 9.81 m/s2 |
Table┬Ā3
3. Results and Discussion
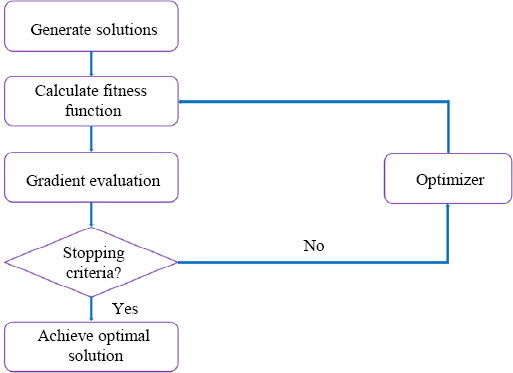
3.1 Optimization of welding process variables using GBO
Table┬Ā4
Table┬Ā5
3.2 Optimization of welding process variables using GPS
Table┬Ā6
Table┬Ā7
3.3 Optimal algorithm selection
4. Conclusion
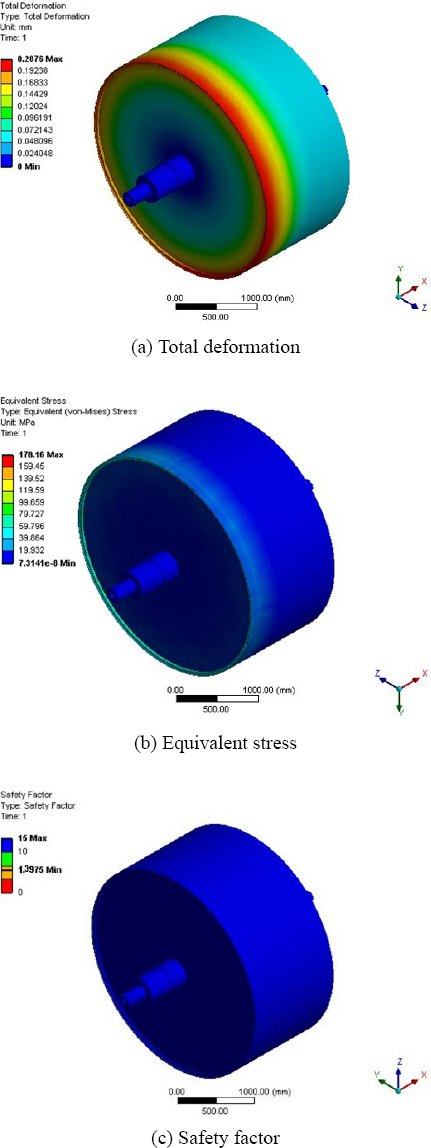
1) As a result of performing thermal elasto-plastic analysis of the titanium drum, the maximum deformation amount of the titanium drum was 0.21 mm in Case 2, and the minimum deformation amount was 0.18 mm in Case 12. The maximum stress appeared at the lower end of the 178.16 MPa titanium drum in Case 1, and the safety factor was the highest at 1.68 in Case 12.
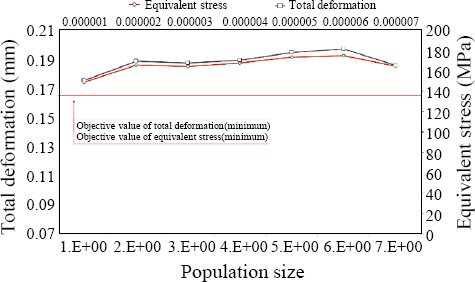
2) The optimal welding process variables for the titanium drum were selected by setting the objective function and limit function of the welding process variables using the GBO technique. The optimal population size that satisfied the safety factor of 1.5 and the minimum deformation amount was selected as 2.E-06. The optimal welding process variables were selected as a welding current of 81.19 A and an arc voltage of 25 V.
3) The optimal welding process variable conditions for the titanium drum were selected by setting the objective function and limit function of the welding process variables using the GPS technique. As the optimal mesh size that satisfied the minimum values of the safety factor and deformation, 3.E-06 was derived. The optimal welding process variables were selected as welding current (89.90 A) and arc voltage (23.92 A).










 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print