1. Introduction
Defects in flux cored arc welding (FCAW) using CO
2 gas causes the increase in the overall quality cost (Q-cost). Destructive and non-destructive inspection methods can be employed for detecting defects, but these methods are not the most effective approach in terms of time and cost. As a more advanced technique, the defects can be detected by welding waveforms
1,2).
However, when unprocessed welding waveforms are examined, it is difficult to distinguish between normal and abnormal waveforms according to the metal transfer mode. This is because waveforms are considerably di- fferent depending on the presence or absence of a short circuit in FACW. Therefore, there is a need for an algorithm that can detect defects from waveforms regardless of the presence of a short circuit.
In this context, the purpose of this study is to develop a defect detection algorithm by using the interval statistical processing method in which information on welding condition shown in the welding current and voltage waveforms is represented in time series.
In the experiment, for bead on plate welding with FCAW, under a constant current condition, the contact tip to work distance (CTWD) and voltage were adjusted to create an unstable welding condition and in this way, the detection algorithm was tested on the presence or absence of the defects for verification of the developed algorithm.
2. Methods
2.1 Materials
The base metal used in this study was SS400 with a length at 150 mm, a width at 125 mm and a thickness at 9 mm, and for the filler metal, ├Ė1.2 mm flux cored wire(AWS A5. 20) was used. Bead on plate welding was performed using Hyosung PFC 600 A DC inverter type welding machine shown in
Fig. 1. For the measurement of welding waveforms, Welteq welding monitoring system shown in
Fig. 2 was used. Signal filtering was performed for proper representation of the welding phenomenon, and the measurement frequency was set to 10 kHz
Fig.┬Ā1
Hyosung PFC 600A DC Inverter power source

Fig.┬Ā2
Welteq arc welding monitoring system

2.2 Experimental method
The length of the welding line on the base metal plate was 130 mm, and the welding speed was 30 cm/min.
Table 1 shows the experimental conditions in which different values of CTWD were set according to the voltage.
Table┬Ā1
Bead on plate experiment condition
|
Filler metal |
AWS A5.20 E71T-1C 1.2 mm |
|
Base metal |
SS400 150 x 125 x 9 mm |
|
Shield gas |
100% CO2 (15 L/min) |
|
Current |
200 A |
|
Welding speed |
30 cm/min |
|
Voltage [V] |
19, 21.5, 24, 26.5, 29 |
|
CTWD [mm] |
10, 15, 20, 25, 30 |
3. Result and Discussion
3.1 Analysis of relationship between welding waveforms and defects
In this study using FCAW for welding, with reference to the short circuit time of 10ms, if the time was shorter than 10ms, the case was defined as normal short circuit, and if the time was longer, it was defined as prolonged short circuit
3).
Fig. 3 shows the welding waveforms and radiographic test (RT) film results when the welding was performed under conditions of 29.0 V in voltage with the reference CTWD 15 (hereinafter condition A). The figure shows the case of a free flight without short circuit, and no defects were identified.
Fig.┬Ā3
Waveform and RT film of condition A
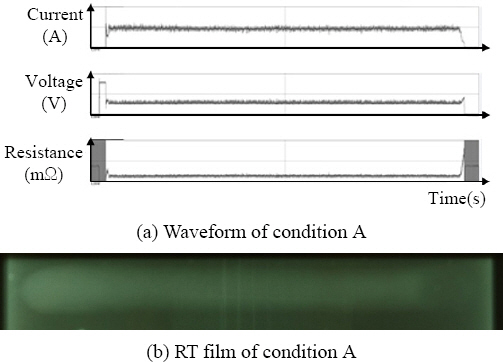
Fig. 4 shows the welding waveforms and RT film results when the welding was performed under conditions of 19.0 V in voltage with CTWD value of 15 (hereinafter condition B). In this figure, multiple cases of short circuit occurred but no defects were identified
Fig.┬Ā4
Waveform and RT film of condition B
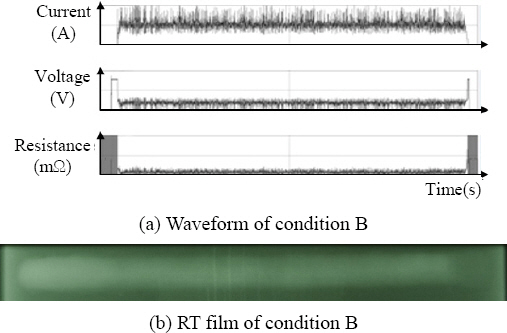
Fig. 5 shows the welding waveforms and RT film results when the welding was performed under conditions of 19.0 V in voltage with CTWD at 20 (hereinafter condition C). In this study, the C level defined in the ISO 5817 specification was used as a reference, and defects that are larger than this level are represented in red in
Fig. 5(b) for visualization. In this case, it can be seen that defects occurred in case of prolonged short circuit and at locations of arc-extinguish.
Fig.┬Ā5
Waveform and RT film of condition C

3.2 Defect occurrence modeling through waveform analysis
Fig. 6 shows the enlarged waveform for 0.5 seconds under condition C in which the short circuits were shown. The interval (b
1-b
2) is a place where the short circuit lasted for 17 ms and is classified as prolonged short circuit.
Fig.┬Ā6
Waveform of long term short circuit transfer (Condition C for 0.5 s)
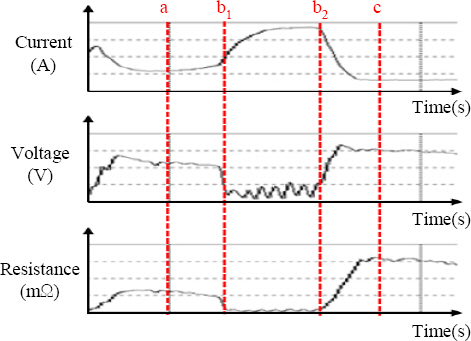
Fig. 7 illustrates the melting phenomenon of the wire in case of prolonged short circuit. Due to the prolonged short circuit, overheating occurred from the resistance heating of the wire, which led to buckling in the middle location, and the wire is separated as in (b
2)
4,5), resulting in arc strike and in this case, the arc length is longer than case of the normal welding. As a result, the voltage increased and the current decreased, resulting in a large resistance value. However, in reality, it was thought that the large resistance was obtained due to the long arc length, and as a result, the current decreased sharply and the voltage increased slightly. In this case, with long arc length under low current, the current density becomes too small, which makes melting of the base metal difficult, and this leads to the risk of lack of fusion or generation of weld pores.
Fig.┬Ā7
Schematics of prolonged short circuit

Fig. 8 shows the enlarged waveform for 0.5 seconds under condition C in which arc-extinguish occurred.
Fig. 9 illustrates the melting phenomenon of the wire in case of art-extinguish occurrence. In (a), after prolonged short circuit, sticking of the wire overheated due to the resistance heating occurred, leading to the buckling of wire at the contact tup end, leading to the separation of wire as shown in (b
1)
4,5). At this time, arc is extinguished (b
1), leading to lack of fusion or generation of weld pores. Subsequently, the wire is slowed down for arc restrike (b
2), contacting the base metal and resulting in the arc restrike (c). During the wire slow-down, the current is 0, no-load voltage occurs, and the resistance is infinite.
Fig.┬Ā8
Waveform of arc extinguish(Condition C for 0.5

Fig.┬Ā9
Schematics of extinguished arc by wire sticking

3.3 Analysis of welding waveforms by interval statistical processing method
3.3.1 Overview of interval statistical processing method
The interval statistical processing is a method pro- posed in this study, and it was defined that in this method, time series is divided into multiple intervals of a short time and statistical processing is performed separately for each interval to evaluate the welding stability for each interval of short time, enabling defect detection.
In the welding waveforms of FCAW, the current, voltage, and resistance vary rapidly with the metal transfer phenomenon occurring for a short duration
7,8). Therefore, welding data needs to be processed for analysis to detect defects using waveforms.
In the interval statistical processing method, the optimal interval length should be set in consideration of the frequency characteristics of the welding. If the interval is set to be too short, the normal short circuit and the prolonged short circuit cannot be distinguished, and if the interval is set to be too long, the defect detection accuracy is lowered. Therefore, this interval has the Nominal-the-best (NTB) characteristic.
In this section, in order to determine the optimal interval for defect detection using the waveforms of the welding resistance that increases 1) immediately after the prolonged short circuit and 2) at arc-extinguish, interval statistical processing was performed with the 5-sec data of conditions A, B, and C compared in Chapter 3 and compared after the processing.
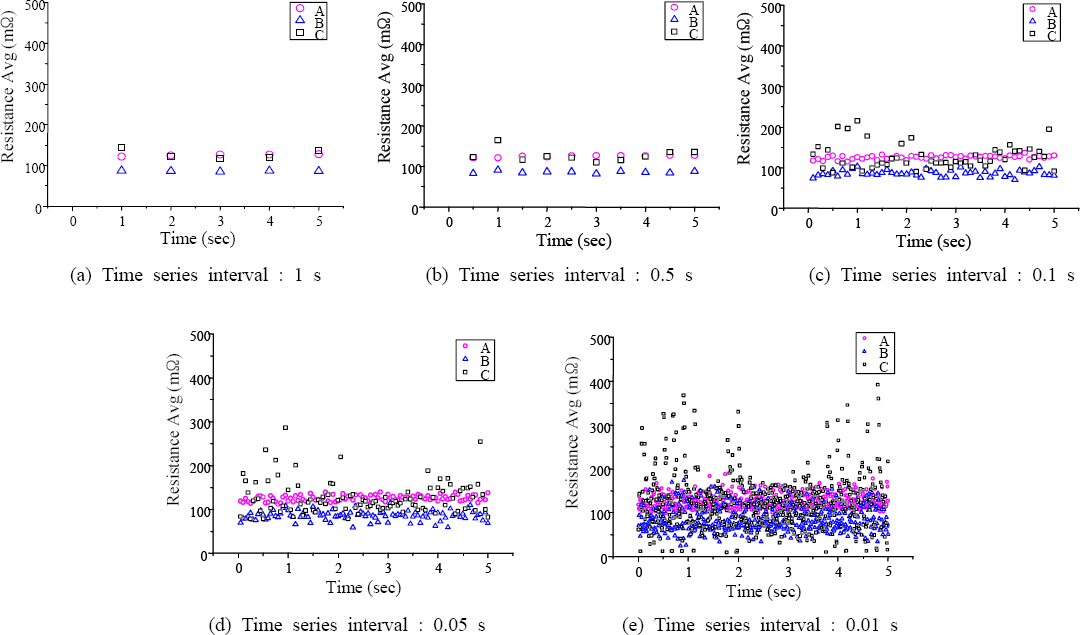
Fig. 10 shows the welding resistance waveforms and RT film results of conditions A, B, and C used for interval statistical processing. Using the welding monitoring system, 50,000 of 5-sec resistance data were analyzed acquired at a sampling rate of 10 kHz per second, and a total of 5 sizes intervals were comparatively analyzed which are 1 second, 0.5 seconds, 0.1 seconds, 0.05 seconds, and 0.01 seconds for analysis of the optimal time series interval.
Fig.┬Ā10

3.3.2 Result of interval statistical processing
For 5-sec duration data of defects in
Fig. 10, in
Fig. 11, further division of intervals into 1.0, 0.5, 0.1, 0.05 and 0.01 sec was performed and the average welding resistance R
avg was represented for each small time series interval. In (a), and (b), the distinction between the defect part and non-defective part was not clear, and in (e), for 5-sec duration, stable data was obtained around 3 sec interval but in case of 1-2 sec intervals and 4-5 sec intervals, data with values twice higher than the stable average value was obtained, indicating that the data in these intervals were unstable. In this study, it was thought that defects may occur in the intervals where these high-value data are obtained. On the other hand, (d) did not show the distinctive characteristic of high value data.
Fig.┬Ā11
Interval statistic results of resistance average
Figs.
12-
14 show the standard deviation, maximum, and minimum of welding resistance, respectively, for each size of interval.
Fig.┬Ā12
Interval statistic results of resistance st.dev

Fig.┬Ā13
Interval statistic results of resistance max
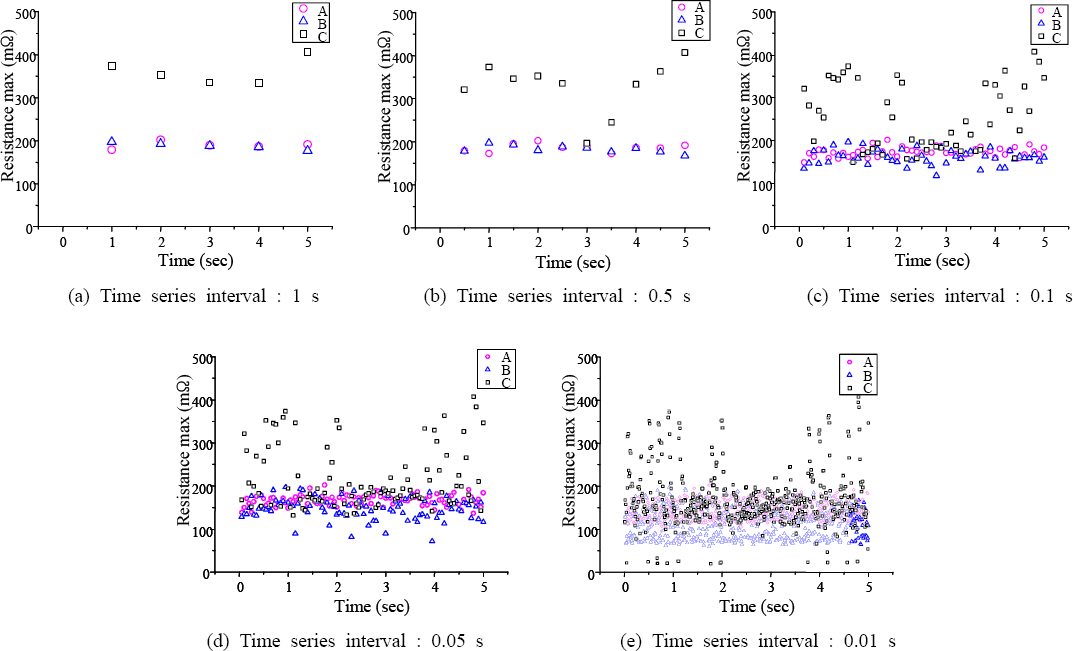
Fig.┬Ā14
Interval statistic results of resistance min
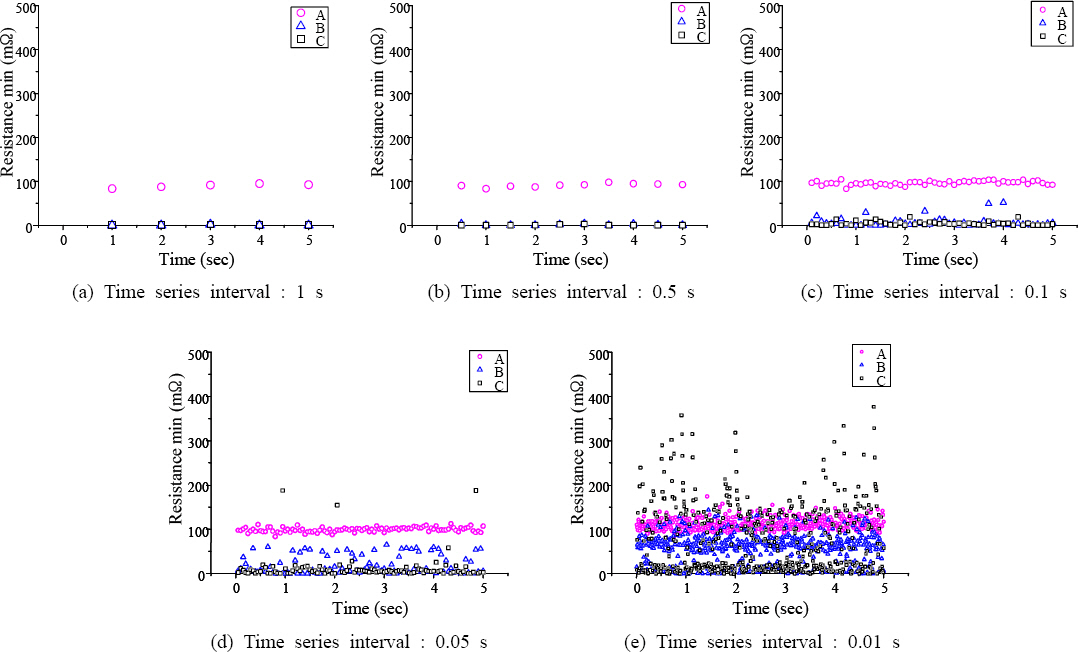
Table 2 shows the results of the interval statistical processing of resistance waveforms by comparing for each time series interval. As a result of analyzing resis- tance_avg, the defect detection result showed a high level of agreement at time series intervals of 0.05 sec and 0.01 sec. As a result of analyzing resistance_st dev, the defect detection result showed a high level of agreement at time series interval of 0.05 sec. As a result of analyzing resistance_max, the defect detection result showed a high level of agreement at time series intervals of 0.1 sec, 0.05 sec and 0.01 sec. As a result of analyzing resistance_min, the defect detection result showed a high level of agreement at time series interval of 0.01 sec.
Table┬Ā2
Comparison of the correspondence for defect detection
|
Time series interval (s) |
|
1 |
0.5 |
0.1 |
0.05 |
0.01 |
|
Ravg
|
Low |
Low |
Middle |
High |
High |
|
Rst.dev
|
Low |
Low |
Low |
High |
Low |
|
Rmax
|
Low |
Low |
High |
High |
High |
|
Rmin
|
Low |
Low |
Low |
Low |
High |
When resistance_max was analyzed, defect detection was possible in all intervals at 0.01 sec, 0.05 sec and 0.1 sec, but in terms of data processing efficiency, 0.1 sec interval was determined to be most optimum.
Therefore, for defect detection, the analysis parameter showing the highest performance of detection when compared to the actual locations of defects is resistance_max and in this case, the optimal time series interval is thought to be 0.1 sec.
Hong
6) proposed a welding defect analysis method with application of moving average filter to welding data for quality analysis of welded parts. At sampling frequency of 10 kHz, 2000 data were selected and processed to remove signal irregularities. In this case, it is considered that it may be difficult to evaluate the instability of a specific interval because the welding signal values generated in the interval are averaged.
However, in this study, a basic algorithm to determine the presence/absence and location of defects was developed using the maximum arc resistance (arc length) obtained with 0.1 sec interval.
4. Conclusion
In this study, for FCAW of carbon steel, a defect detection algorithm was developed by the interval statistical processing method of the arc welding waveforms and the detection result was compared with the RT result of the sample with defects. The following conclusions were derived from the analysis.
1) The results of this study presented that after the occurrence of prolonged short circuit, at arc restrike, the arc length was longer, leading to considerably low current and large resistance, and this resulted in lack of fusion or generation of weld pores.
2) When the arc is extinguished by wire sticking, the current is 0, a no-load voltage occurs, and the resistance becomes infinite. Therefore, the detection of the arc- extinguish can be easily performed through resistance waveforms, and the arc-extinguish resulted in lack of fusion or generation of weld pores.
3) When using resistance_max for each interval in the welding waveforms, defect detection was achieved in all intervals at 0.01 sec, 0.05 sec, and 0.1 sec and in consideration of data processing efficiency, 0.1 sec interval was determined to be the optimal duration of the interval.
Acknowledgements
We acknowledge that this study is funded by research grant from KEIT, South Korean Ministry of Trade, Industry and Energy. [No : 20003633]
References
1. T. Quinn, C. Smith, C. McCowan, E. Blachowiak, and R. Madigan, Arc sensing for defects in constant-voltage Gas Metal Arc Welding, Weld. J. 79 (1999) 322ŌĆō328.
2. S. Adolfsson, A. Bahrami, G. Bolmsjo, and I. Claesson, On-line quality monitoring in short circuit gas metal arc welding, Weld. J. 78 (1999) 59ŌĆō73.
3. Y. Chu, S. Hu, W. Hou, P. Wang, and S. Marin, Signature analysis for quality monitoring in short-circuit GMAW, Weld. J. 83 (2004) 336ŌĆō343.
4. D. Farson, C. Conardy, J. Talkington, K. Baker, T. Kerschbaumer, and P. Edwards, Arc initiation in Gas Metal Arc Welding, Weld. J. 77 (1998) 315ŌĆō321.
5. E. Choi, J. Y. Kim, S. H. Shin, and S. Y. Kim, A study on the analysis effectiveness of the virtual welding simulator for welding manpower development,
J. Weld. Join. 33(3) (2015) 40ŌĆō46. https://doi.org/10.5781/JWJ.2015.33.3.40
[CROSSREF] 6. W.H. Hong and J. T. Ryu, A study on the welding current and voltage signal processing method for the quality evaluation of robotic GMAW,
J. Korea Industr. Inf. Syst. Res.(KSIIS). 19(6) (2014) 321ŌĆō325. https://doi.org/10.9723/jksiis.2014.19.6.025
[CROSSREF] 7. B.W. Seo, Y. C. Jeong, and Y. T. Cho, A study on the Selection of Arc Sensing Signal for Seam Tracking in Pulsed GMAW,
J. Weld. Join. 38(2) (2020) 173ŌĆō179. https://doi.org/10.5781/JWJ.2020.38.2.7
[CROSSREF] 8. J.Y. Park and S. H. Song, Study on the Evaluation of Weld Soundness Based on Arc Stability and Bead Quality using the Statistical Analysis of Arc Power and Arc Dynamic Resistance,
J. Weld. Join. 37(6) (2019) 599ŌĆō604. https://doi.org/10.5781/JWJ.2019.37.6.10
[CROSSREF]


















 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print