1. ņä£ ļĪĀ
ņĄ£ĻĘ╝ ņäĀļ░Ģ, ļ╣äĒ¢ēĻĖ░ņÖĆ ļŹöļČłņ¢┤ ņżæņÜö ņÜ┤ņåĪņłśļŗ©ņżæ ĒĢśļéśņØĖ ņ×ÉļÅÖņ░©ļŖö ņŚ░ļ╣äĒ¢źņāü ļ░Å ņĢłņĀäĻĘ£ņĀ£Ļ░Ć Ļ░ĢĒÖöļÉśņŚłļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ ĻĄŁļé┤ņÖĖ ņ×ÉļÅÖņ░©ņé¼ņŚÉņä£ļŖö ņĢłņĀäņŚÉļÅä ļ¼ĖņĀ£Ļ░Ć ņŚåņ£╝ļ®░ ņŚÉļäłņ¦Ć ĒÜ©ņ£©ņØä ĻĘ╣ļīĆĒÖöĒĢĀ ņłś ņ׳ļŖö ņ░©ņ▓┤ņØś Ļ▓Įļ¤ēĒÖöļź╝ ļ¬®Ēæ£ļĪ£ ĒĢśĻ│Ā ņ׳ļŗż. ņ░©ņ▓┤ļź╝ Ļ▓Įļ¤ēĒÖö ĒĢśņŚ¼ ņŚÉļäłņ¦Ć ĒÜ©ņ£©ņØä ļåÆņØ┤ļŖö ļīĆĒæ£ņĀüņØĖ ļ░®ļ▓Ģņ£╝ļĪ£ļŖö ĻĖ░ņĪ┤ Ļ░ĢĒīÉņØä Ļ│ĀĻ░ĢļÅä Ļ░ĢĒīÉņ£╝ļĪ£ ļ░öĻŠĖĻ│Ā ļæÉĻ╗śļź╝ ņżäņØ┤ļŖö ļ░®ļ▓ĢņØ┤ ņŻ╝ļĪ£ ņé¼ņÜ®ļÉ£ļŗż. ņØ┤ņŚÉ ļö░ļØ╝ Ļ░ĢĒīÉņØś ļŗżņ¢æĒĢ£ Ļ░ĢņóģņØ┤ Ļ░£ļ░£ļÉśņŚłļŖöļŹ░ ļīĆĒæ£ņĀüņØĖ ņśłļĪ£ DP (Dual Phase)Ļ░Ģ, CP(Complex Phase)Ļ░Ģ,MSĻ░Ģ(Mar- tensitic)Ļ░Ģ, TRIP(Transformation Induced Plasticity) Ļ░Ģ, TWIP(Twinning Induced Plasticity)Ļ░Ģ ļō▒ņØ┤ ļīĆĒæ£ņĀüņØĖ ņØĖņןĻ░ĢļÅä 700MPa ņØ┤ņāüņØś AHSS (Advanced High Strength Steel)Ļ░ĢņØ┤ļ®░ 1500MPaĻĖē ņØ┤ņāüņØś UHSS(Ultra High Strength Steel)ņØ┤ļŗż. ņØ┤ņÖĆ Ļ░ÖņØĆ Ļ│ĀĻ░ĢļÅä Ļ░ĢĒīÉ ļ░Å ņ┤łĻ│ĀĻ░ĢļÅä Ļ░ĢĒīÉņØś ņĀüņÜ®ņØ┤ ņ”ØĻ░ĆĒĢśĻ│Ā ņ׳ļŗż
1).
Ļ│ĀĻ░ĢļÅäĻ░ĢņØä ņ░©ņ▓┤ņŚÉ ņĀüņÜ®ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ņÜ®ņĀæĻ│ĄņĀĢņØ┤ ĒĢäņłśņĀüņØ┤ļ®░, ņøÉĻ░Ć ņĖĪļ®┤ņŚÉņä£ ņ£Āļ”¼ĒĢ£ ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ(resistance spot welding)ņØ┤ ņ░©ņ▓┤ ņÜ®ņĀæņŚÉņä£ 80%ņØ┤ņāüņ£╝ļĪ£ Ļ░Ćņן ļ¦ÄņØ┤ ņĀüņÜ®ļÉśĻ│Ā ņ׳ļŗż
2).
ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņä▒ņØä ĒÅēĻ░ĆĒĢśĻ▒░ļéś ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ Ēøä ņÜ®ņĀæļČĆ Ļ░ĢļÅä ļ░Å ļäłĻ▓¤ ņ¦Ćļ”äņŚÉ ļīĆĒĢ£ ĒÅēĻ░Ć Ļ▓░Ļ│╝ļŖö ņ░©ņ▓┤ņØś ņäżĻ│äņŚÉ ļ¦żņÜ░ ņżæņÜöĒĢ£ ļŹ░ņØ┤Ēä░ļź╝ ņĀ£Ļ│ĄĒĢĀ ņłś ņ׳ļŗż. ņ┤łĻ│ĀĻ░ĢļÅäĻ░ĢņØĆ Ļ░ĢļÅäĒ¢źņāüņØä ņ£äĒĢ┤ ĒĢ®ĻĖłņøÉņåī ĒĢ©ļ¤ēņØä ļŖśņØ┤ĻĖ░ ļĢīļ¼ĖņŚÉ ņØ╝ļ░śņĀüņ£╝ļĪ£ ņÜ®ņĀæņä▒ņØ┤ ņŚ┤ņĢģĒĢ£ Ļ▓āņ£╝ļĪ£ ņĢīļĀżņĀĖ ņ׳ļŗż
3). ņØ┤ļ¤¼ĒĢ£ ņ┤łĻ│ĀĻ░ĢļÅäĻ░ĢņØś ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņØś Ļ▓ĮņÜ░ ņĀüņĀĢ ņÜ®ņĀæņĪ░Ļ▒┤ ņśüņŚŁņØ┤ ņČĢņåīļÉśĻ│Ā ņÜ®ņĀæļČĆņŚÉņä£ Ļ│äļ®┤Ēīīļŗ© ļ░Å ļČĆļČäĻ│äļ®┤Ēīīļŗ©ņØ┤ ļ░£ņāØĒĢśļŖö Ļ▓āņ£╝ļĪ£ ļ│┤Ļ│ĀļÉśņ¢┤ ņ׳ņ¢┤ Ļ▓░ĒĢ© ļ░Å ĒÆłņ¦łņØä ņŗżņŗ£Ļ░äņ£╝ļĪ£ ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ņÜ®ņĀæĒÆłņ¦ł ĒīÉņĀĢĻ│╝ Ļ┤ĆļĀ©ļÉ£ ņŚ░ĻĄ¼Ļ░Ć ĒÖ£ļ░£Ē׳ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ļŗż.
ņ░©ņ▓┤ļź╝ ĻĄ¼ņä▒ĒĢśļŖö Ļ░ĢņóģņØś ņóģļźśņÖĆ ļæÉĻ╗śĻ░Ć ļŗżņ¢æĒĢ┤ņ¦ĆĻ│Ā ņ׳ņ£╝ļ®░, ļ¬©ļōĀ Ļ░ĢņóģĻ│╝ ļæÉĻ╗śņŚÉ ļīĆĒĢśņŚ¼ ņŗżĒŚśņŚÉ ņØśņĪ┤ĒĢśņŚ¼ ņÜ®ņĀæņä▒ņØä ĒÅēĻ░ĆĒĢ£ļŗżļ®┤, ļ¦ÄņØĆ ņŗ£Ļ░ä, ļ╣äņÜ® ļō▒ņØ┤ Ēł¼ņ×ÉļÉśņ¢┤ņĢ╝ ĒĢ£ļŗż. ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ņĀÉņØä ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņŗ£ļ«¼ļĀłņØ┤ņģś ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśĻ│Ā ņ׳ļŗż.
ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņØ┤ņÜ®ĒĢ┤ ļŗżņ¢æĒĢ£ Ļ░ĢņóģĻ│╝ ļæÉĻ╗śņŚÉ Ļ┤ĆļĀ©ĒĢśņŚ¼ Ļ░ĢļÅä ļ░Å ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØ┤ Ļ░£ļ░£ļÉ£ļŗżļ®┤ ĻĘĖ ĒÜ©ņ£©ņä▒ņØĆ ļ¦żņÜ░ Ēü¼ļŗżĻ│Ā ļ│╝ ņłś ņ׳ļŗż
4). ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņŚÉņä£ ņØ╝ļ░śņĀüņ£╝ļĪ£ ņÜ®ņĀæņä▒ ĒÖĢņØĖņØä ņ£äĒĢ┤ ļĪ£ļĖīĻ│ĪņäĀņØä ņØ┤ņÜ®ĒĢśļ®░ ņĀüņĀĢ ņÜ®ņĀæ ņĪ░Ļ▒┤ņØä ĻĄ¼ĒĢ£ļŗż
5). ņÜ®ņĀæ ņĪ░Ļ▒┤ņØś ņĄ£ņĀüĒÖöļź╝ ņ£äĒĢ┤ Ļ░ĢļÅäļéś ļäłĻ▓¤ ņ¦Ćļ”äņØś ņśłņĖĪļ¬©ļŹĖņØ┤ ĒĢäņÜöļĪ£ ĒĢśļ®░ ņśłņĖĪ ļ¬©ļŹĖņØä ĒåĄĒĢśņŚ¼ ņÜ®ņĀæņĪ░Ļ▒┤ņØä ņĄ£ņĀüĒÖö ĒĢśļŖö Ļ│╝ņĀĢņØ┤ ĒĢäņÜöĒĢśļŗż. ņØ┤ļ¤░ ņśłņĖĪ ļ¬©ļŹĖņØä ņ£äĒĢ┤ Hong
6) ļō▒ņØĆ ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņØś ņÜ®ņ£ĄļČĆļź╝ ņŗĀĻ▓ĮĒÜīļĪ£ļ¦ØĻ│╝ ĒÜīĻĘĆļ¬©ļŹĖņØä ņé¼ņÜ®ĒĢśņŚ¼ ņśłņĖĪĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ĻĖ░ņĪ┤ ņŚ░ĻĄ¼ļŖö ņŗżĒŚśņØä ļ░öĒāĢņ£╝ļĪ£ ĒĢ£ Ļ▓āņ£╝ļĪ£ ņåīņ×¼ ļŗżņ¢æĒÖöņŚÉ ņĀüĻĘ╣ņĀüņ£╝ļĪ£ ļīĆņØæĒĢĀ ņłś ņŚåļŗżļŖö ĒĢ£Ļ│äĻ░Ć ņ׳ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 1500MPaĻĖē ņ┤łĻ│ĀĻ░ĢļÅä Ļ░ĢĒīÉņŚÉ ļīĆĒĢśņŚ¼ ņŚ¼ļ¤¼ ņóģļźśņÖĆ ļŗżņ¢æĒĢ£ ļæÉĻ╗ś ņĪ░ĒĢ®ņŚÉ ļīĆĒĢ£ ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒåĄĒĢ┤ ņÜ®ņĀæļČĆņØś ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ļśÉĒĢ£ ļŗżņ¢æĒĢ£ ņÜ®ņĀæ ņĪ░Ļ▒┤ņŚÉ ļö░ļØ╝ 1500MPaĻĖē ĒīÉņ×¼ņØś ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒ¢łņ£╝ļ®░, ĻĘĖ Ļ▓░Ļ│╝ ļĪ£ļĖīĻ│ĪņäĀņØä ņ¢╗ņØä ņłś ņ׳ņŚłļŗż. ņÜ®ņĀæļČĆ ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖļĪ£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆņ£╝ļ®░, ņ×ģļĀź ņØĖņ×Éļź╝ ņĄ£ņåīĒÖö ĒĢ£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆļŗż.
2. ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģś
2.1 ņĀĆĒĢŁņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģś ņ¦Ćļ░░ļ░®ņĀĢņŗØ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░ ņØ┤ļź╝ ņ£äĒĢ£ ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ Ēü¼Ļ▓ī ņŚ┤ņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØĻ│╝ ĻĖ░Ļ│äņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØņ£╝ļĪ£ ĻĄ¼ļČäņØ┤ ļÉ£ļŗż. ņŚ┤ņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņĀäļźśņØś ĒåĄņĀäņŚÉ ļö░ļźĖ Ļ░ĆņŚ┤ ļ░Å ņÜ®ņĀæ Ēøä ļāēĻ░üņØś ņś©ļÅäļ│ĆĒÖöļź╝ ņ£äĒĢ£ Ļ▓āņØ┤ļ®░, ĻĖ░Ļ│äņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņÜ®ņĀæ Ēøä ļé┤ļČĆ ņØæļĀźņØś ļ│ĆĒÖöņŚÉ ļö░ļźĖ ĒśĢņāüņØś ļ│ĆĒÖöļź╝ Ļ│äņé░ĒĢśĻĖ░ ņ£äĒĢ£ Ļ▓āņØ┤ļŗż.
ņŚ┤ņĀü ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ GalerkindņØś ņŚ┤ņĀäļŗ¼ ļ░®ņĀĢņŗØņØä ļö░ļź┤ļ®░ ņŗØ (1)Ļ│╝ Ļ░Öļŗż
7).
ņŚ¼ĻĖ░ņä£ kļŖö ņŚ┤ņĀäļŗ¼Ļ│äņłś, TļŖö ņś©ļÅä, VļŖö Ļ┤Ćņŗ¼ ņ▓┤ņĀü(domain volume), pmņØĆ ļ░ĆļÅä, cmņØĆ ļ╣äņŚ┤, qļŖö ļ░£ņŚ┤, SļŖö Ļ▓ĮĻ│ä Ēæ£ļ®┤(boundary surface), ŌłÅļŖö ĻĖ░Ļ│äņĀü ĒלņŚÉ ņØśĒĢ£ ņŚÉļäłņ¦Ćļź╝ ļéśĒāĆļéĖļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ Ļ░üĻ░üņØś ĒĢŁņØĆ ļ░£ņāØ ņÜöņØĖ Ēś╣ņØĆ ņ£äņ╣śņŚÉ ļö░ļØ╝ ņŚ┤ņĀäļŗ¼ņØä Ēæ£ĒśäĒĢ£ Ļ▓āņ£╝ļĪ£ ņ▓½ ļ▓łņ¦Ė ĒĢŁņØĆ ņŚ┤ņĀäļÅäņŚÉ ņØśĒĢ£ ņŚÉļäłņ¦Ć, ļæÉ ļ▓łņ¦Ė ĒĢŁņØĆ ļé┤ļČĆņŚÉ ņĀĆņןļÉśļŖö ņŚÉļäłņ¦Ć, ņäĖ ļ▓łņ¦Ė ĒĢŁņØĆ ļ»Ėņåī ļ│╝ļź©ņŚÉņä£ņØś ņĀäĻĖ░ņĀü ļ░£ņŚ┤ ņŚÉļäłņ¦Ć, ļäż ļ▓łņ¦Ė ĒĢŁņØĆ Ēæ£ļ®┤ņŚÉņä£ ļ░£ņāØĒĢśļŖö ļ░£ņŚ┤ ņŚÉļäłņ¦ĆņØ┤ļ®░, ļŗżņä» ļ▓łņ¦Ė ĒĢŁņØĆ ļ¦łņ░░ ļ░Å ĻĖ░Ļ│äņĀüņØĖ ĒלņŚÉ ņØśĒĢ£ ļ░£ņŚ┤ Ēś╣ņØĆ ņŚ┤ņĀü ņåīņé░ ņŚÉļäłņ¦Ćļź╝ ļéśĒāĆļéĖļŗż.
ĻĖ░Ļ│äņĀü ļ¬©ļŹĖņØś ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņŗØ (2)ņÖĆ Ļ░Öļŗż
7).
ņŚ¼ĻĖ░ņä£, Žā┬»ļŖö ņ£ĀĒÜ© ņØæļĀź(effective stress)ņØ┤Ļ│Ā, KļŖö ĒÄśļäÉĒŗ░ ņāüņłś(factor), ╬Ą┬»╦Ö,╬Ą╦ÖijļŖö Ļ░üĻ░ü ņ£ĀĒÜ© ļ│ĆĒśĢņ£©(effective strain)Ļ│╝ ļ│ĆĒśĢņ£© ĒģÉņä£(strain rate tensor)ņØ┤ļŗż. tļŖö ņŗ£Ļ░äņØ┤ļ®░, uļŖö ļ│Ćņ£äļź╝ ļéśĒāĆļéĖļŗż. ņ▓½ ļ▓łņ¦Ė ĒĢŁņØĆ ĒĢ┤ņäØ ņśüņŚŁ ļé┤ņŚÉņä£ ņåīņä▒ ļ│ĆĒśĢņŚÉ ļö░ļźĖ ņŚÉļäłņ¦Ć ļ│ĆĒÖöņ£©, ļæÉ ļ▓łņ¦Ė ĒĢŁņØĆ ļ╣äņĢĢņČĢņä▒ ĻĄ¼ņåŹņĪ░Ļ▒┤ņŚÉ Ļ┤ĆĒĢ£ ņŚÉļäłņ¦Ć ļ│ĆĒÖöņ£©ļĪ£ ĒÄśļäÉĒŗ░ ņāüņłśņŚÉ ņØśĒĢ┤ ĻĄ¼ņåŹņĪ░Ļ▒┤ņØś ņŚ¼ļČĆņŚÉ ļö░ļØ╝ ĒÖ£ņä▒ĒÖöļÉĀ ņłś ņ׳ļŗż. ņäĖ ļ▓łņ¦Ė ĒĢŁņØĆ ļ¦łņ░░ņŚÉ ļö░ļØ╝ ļ░£ņāØĒĢśļŖö ņŚÉļäłņ¦Ć ļ│ĆĒÖöņ£©, ļäż ļ▓łņ¦Ė ĒĢŁņØĆ ņĀæņ┤ēņŚÉ ļö░ļźĖ ņŚÉļäłņ¦Ć ļ│ĆĒÖöņ£©ņØ┤ļŗż.
ņØ┤ņÖĆ Ļ░ÖņØĆ ņŗ£ļ«¼ļĀłņØ┤ņģśņØś ņ¦Ćļ░░ļ░®ņĀĢņŗØņØĆ ņä£ļĪ£ ņŚ░ņä▒ļÉśņ¢┤ ņ׳ņ¢┤ ņłśļ¦ÄņØĆ ļ░śļ│ĄĻ│╝ņĀĢņØä ĒåĄĒĢ┤ Ļ░üĻ░üņØś ļ®öņē¼ņŚÉ ļīĆĒĢ£ ĒÆĆņØ┤ļź╝ ņłśĒ¢ēĒĢśĻ▓ī ļÉ£ļŗż. ņŗ£ļ«¼ļĀłņØ┤ņģśņŚÉņä£ ņé¼ņÜ® ļÉśņ¢┤ņ¦ä ņ×¼ļŻīņÖĆ ņĀäĻĘ╣ņØĆ ĒśäņןņŚÉņä£ ņō░ņØ┤ļŖö Ļ▓āņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņŚ¼ Ļ░ü ņåīņ×¼ ļŹ░ņØ┤Ēä░ļź╝ ņ×ģļĀźņ£╝ļĪ£ ņé¼ņÜ®ĒĢśņśĆļŗż.
ņĀäĻĘ╣ ļ░Å ĒīÉņ×¼ņŚÉ ļīĆĒĢ£ ļ¬©ļŹĖļ¦üņØĆ
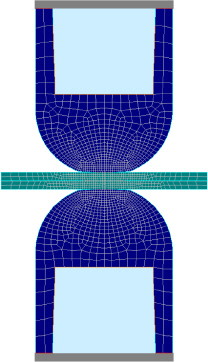
Fig. 1Ļ│╝ Ļ░Öņ£╝ļ®░, ļ¬©ļŹĖņØś ļ®öņē¼ ĒśĢĒā£ļŖö 4Ļ░ü ļ®öņē¼ ĒśĢĒā£ļź╝ ņØ┤ņÜ®ĒĢśņśĆĻ│Ā, ņĀĢĒÖĢĒĢ£ Ļ│äņé░ņØä ņ£äĒĢ┤ ņĀæņ┤ēļČĆņØś ļ®öņē¼ņØś Ēü¼ĻĖ░ļź╝ ņ×æĻ▓īĒĢśņŚ¼ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢśņśĆļŗż.
Fig.┬Ā1
Mesh of steel sheet and electrode for numerical simulation
2.2 ņĀĆĒĢŁņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģś ņĪ░Ļ▒┤
ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņ£äĒĢ£ ņĪ░Ļ▒┤ņ£╝ļĪ£ ņé¼ņÜ®ļÉ£ ņÜ®ņĀæĻĖ░ļŖö 60Hz ĻĄÉļźśņÜ®ņĀæĻĖ░ļĪ£ ņäżņĀĢĒĢśņśĆņ£╝ļ®░, ņé¼ņÜ®ļÉ£ ņĀäĻĘ╣ņØĆ ņØ╝ļ░śņĀüņØĖ ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņŚÉ ļ¦ÄņØ┤ ņō░ņØ┤ļŖö ļÅöĒśĢ ņĀäĻĘ╣ņ£╝ļĪ£ ņ¦üĻ▓Į 16mm, ņäĀļŗ©Ļ▓Į 6mmņØĖ CuCrņåīņ×¼ņØś ņĀäĻĘ╣ņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ļāēĻ░üņłśļŖö 20┬░CļĪ£ 4l/minņØś ņ£Āļ¤ēņ£╝ļĪ£ ņĀäĻĘ╣ņŚÉ ĒØÉļź┤ļÅäļĪØ Ļ▓ĮĻ│äņĪ░Ļ▒┤ņØä ņäżņĀĢĒĢśņśĆļŗż.
ņŗ£ļ«¼ļĀłņØ┤ņģśņŚÉ ņé¼ņÜ®ļÉ£ ņ×¼ļŻīļŖö 1500MPaĻĖē ĒĢ½ņŖżĒā¼ĒĢæ ļ│┤ļĪĀĻ░Ģ (HS1500) 1.0mmņÖĆ 1.4mm ļæÉĻ╗śļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. ņØ┤ņóģ Ļ░Ģņ×¼ņØś ņĪ░ĒĢ®ņŚÉ ļö░ļźĖ ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņ£äĒĢ┤ņä£ ņČöĻ░ĆņĀüņ£╝ļĪ£ DP590 1.0mmņÖĆ 1.4mm ĻĘĖļ”¼Ļ│Ā DP780 1.0mmņÖĆ 1.4mmņØś Ļ░Ģņ×¼ļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. Ļ░üĻ░ü ļæÉĻ╗ś ņĪ░ĒĢ®ņŚÉ ļö░ļźĖ ļÅÖņóģ ļ░Å ņØ┤ņóģĻ░ĢņóģņŚÉ ļīĆĒĢ£ ņĪ░ĒĢ®ņ£╝ļĪ£ ņ┤Ø 7Ļ░Ćņ¦Ć ņĪ░ĒĢ®ņŚÉ ļīĆĒĢśņŚ¼
Table 1Ļ│╝ Ļ░ÖņØĆ ņÜ®ņĀæņĪ░Ļ▒┤ņ£╝ļĪ£ ņŗ£ļ«¼ļĀłņØ┤ņģś ĒĢśņśĆĻ│Ā Ļ░ü ņ×¼ļŻīņØś ĒÖöĒĢÖņĀü ņä▒ļČäņØĆ
Table 2ņÖĆ Ļ░Öļŗż.
Table┬Ā1
|
Variables |
Minimum value |
Maximum value |
Increase value |
|
Current (kA) |
3 |
11 |
1 |
|
Force (kgf) |
200 |
400 |
100 |
|
Time (Cycle) |
12 |
24 |
3 |
Table┬Ā2
Chemical composition (wt%)
|
Steel |
C |
Mn |
Si |
Cr |
Mo |
B |
Fe |
|
HS1500 |
0.235 |
1.3 |
0.25 |
0.155 |
- |
0.0037 |
Re |
|
DP590 |
0.095 |
1.9 |
0.16 |
- |
0.09 |
- |
Re |
|
DP780 |
0.07 |
2.4 |
1.05 |
0.1 |
0.03 |
- |
Re |
3. ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝
ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņŚÉņä£ ņÜ®ņĀæņä▒ņØä Ēæ£ĒśäĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ ņŻ╝ļĪ£ ņé¼ņÜ®ļÉśļŖö ļ░®ļ▓ĢņØ┤ ļĪ£ļĖīĻ│ĪņäĀņØä ĒÖ£ņÜ®ĒĢ£ļŗż
8). ņØ╝ļ░śņĀüņ£╝ļĪ£ ļĪ£ļĖīĻ│ĪņäĀņØĆ ISO-14327ņŚÉ ļö░ļØ╝ ļÅäņČ£ĒĢśļ®░ ĻĖ░ņĪ┤ ņŚ░ĻĄ¼
9)ņŚÉņä£ļŖö 3.5
tņ£╝ļĪ£ ĒĢśļéś ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 4
tņØś ļäłĻ▓¤ ņ¦Ćļ”äņØä ņĄ£ņåī ĒŚłņÜ® ļäłĻ▓¤ ņ¦Ćļ”äņØä ĻĖ░ņżĆņ£╝ļĪ£ ĒĢśņśĆļŗż.
ņŗ£ļ«¼ļĀłņØ┤ņģśņØś Ļ▓░Ļ│╝ļŖö ņŗżņĀ£ ņÜ®ņĀæ Ļ▓░Ļ│╝Ļ░Ć ļ¦żņÜ░ ņ£Āņé¼ĒĢ£ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłĻ│Ā
10-13), ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņŗżĒŚśņĀü ļ░®ļ▓ĢņØ┤ ņĢäļŗī ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņÜ®ņĀæļČĆ ļäłĻ▓¤ņØś ņ¦Ćļ”äņØä ņĖĪņĀĢĒĢśņśĆļŗż.
Fig. 2ļŖö HS1500 1.0mmņØś ļÅÖņóģņåīņ×¼ņŚÉ ļīĆĒĢ£ ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ņØ┤ļŗż.
Fig. 2ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ Ļ░ĆļĪ£ņČĢņØĆ ņÜ®ņĀæ ņĀäļźśĻ░Ć ņäĖļĪ£ņČĢņØĆ ņÜ®ņĀæ ņŗ£Ļ░äĻ│╝ Ļ░ĆņĢĢļĀźņØ┤ Ēæ£ņŗ£ļÉśņ¢┤ ņ׳ņ£╝ļ®░, Ļ░ü ņĪ░Ļ▒┤ļ│äļĪ£ ņÜ®ņĀæļČĆ ļäłĻ▓¤ņØś ņ¦Ćļ”äņØ┤ ņł½ņ×ÉļĪ£ Ēæ£ņŗ£ļÉśņ¢┤ ņ׳ļŗż. ĻĘĖļ”╝ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ņĀäļźśĻ░Ć ņ╗żņ¦łņłśļĪØ ņÜ®ņĀæņŗ£Ļ░äņØ┤ ĻĖĖņ¢┤ņ¦łņłśļĪØ ĻĘĖļ”¼Ļ│Ā Ļ░ĆņĢĢļĀźņØ┤ ņ×æņĢäņ¦łņłśļĪØ ņÜ®ņĀæļČĆ ļäłĻ▓¤ņØś Ēü¼ĻĖ░Ļ░Ć ņ╗żņ¦ĆĻ│Ā ņ׳ļŗż. ņŗżĒŚśņŚÉ ņé¼ņÜ®ļÉ£ ĻĘĖļ”╝ņŚÉņä£ Ļ░üĻ░üņØś ņÜ®ņĀæņĪ░Ļ▒┤ņŚÉ ļö░ļźĖ ņÜ®ņĀæļČĆ ļäłĻ▓¤ ņ¦Ćļ”ä Ļ░ÆņØä ļéśĒāĆļé┤ņŚłĻ│Ā, ņÖ╝ņ¬ĮņØĆ ļäłĻ▓¤ņØś ĒśĢņä▒ņØ┤ ļÉśņ¦Ć ņĢŖļŖö Ļ▓ĮņÜ░ Ēś╣ņØĆ ņĄ£ņåī ĒŚłņÜ® ļäłĻ▓¤ ņ¦Ćļ”ä ļ│┤ļŗż ļé«ņØĆ ĻĄ¼Ļ░äņØ┤ļ®░, ņāüĒĢ£ņØś Ļ▓ĮņÜ░ļŖö ņŖżĒī©Ēä░Ļ░Ć ļ░£ņāØĒĢ£ ĻĄ¼Ļ░äņØ┤ļŗż.
Fig. 3ņØĆ HS1500 1.0tņØś ļĪ£ĻĘĖĻ│ĪņäĀņØ┤ļŗż. ļĪ£ļĖīĻ│ĪņäĀņŚÉņä£ ļäłĻ▓¤ ņ¦Ćļ”ä ļ»Ėļŗ¼, ņĀüņĀĢ ņÜ®ņĀæĻĄ¼Ļ░ä, ļ░Å ņŖżĒī©Ēä░ ņśüņŚŁņØä Ļ░üĻ░üņØś ņāēĻ╣öļĪ£ ĻĄ¼ļČäĒĢśņśĆļŗż. ļäłĻ▓¤ ņ¦Ćļ”ä ļ»Ėļŗ¼ņśüņŚŁņØĆ ĒÜīņāēņ£╝ļĪ£ ņŖżĒī©Ēä░ ņśüņŚŁņØĆ ņĀüņāē ĻĘĖļ”¼Ļ│Ā ņżæĻ░äļČĆļČäņØĖ ņĀüņĀĢ ņÜ®ņĀæĻĄ¼Ļ░äņØĆ ļģ╣ņāēņ£╝ļĪ£ Ēæ£ĒśäĒĢśņśĆļŗż.
Fig.┬Ā2
Nugget diameter for HS1500 steel sheets according to welding conditions
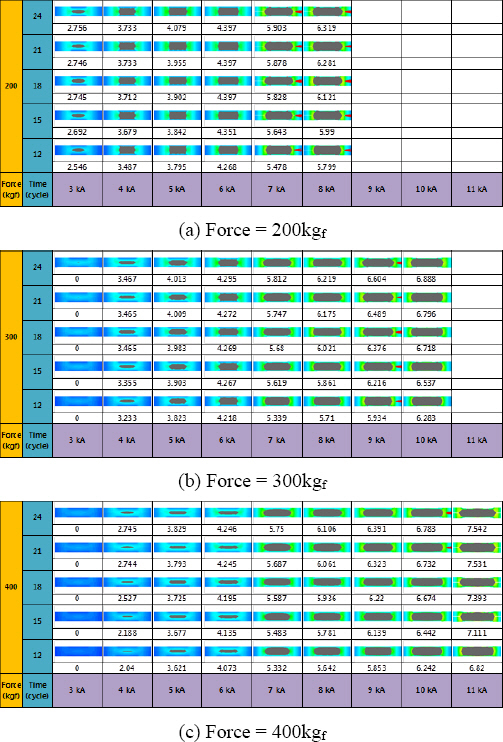
Fig.┬Ā3
Welding lobe curve for HS15001.0mm sheets
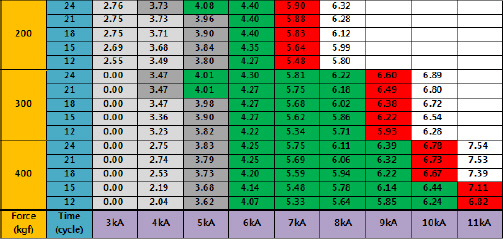
ļĪ£ļĖīĻ│ĪņäĀņŚÉņä£ Ļ░ĆņĢĢļĀźņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ ļäłĻ▓¤ņØś ņ¦Ćļ”äņØĆ Ļ░ÉņåīĒĢśļŖöļŹ░ ņØ┤Ļ▓āņØĆ Ļ░ĆņĢĢļĀźņØ┤ ņ”ØĻ░ĆĒĢśļ®┤ņä£ ņĀæņ┤ēņĀĆĒĢŁņØ┤ Ļ░ÉņåīĒĢśĻ│Ā ņØ┤ļĪ£ ņØĖĒĢśņŚ¼ ņÜ®ņĀæļČĆņØś ļ░£ņŚ┤ņØ┤ Ļ░ÉņåīĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ Ļ░ĆņĢĢļĀźņØ┤ ņ╗żņ¦łņłśļĪØ ļĪ£ĻĘĖĻ│ĪņäĀņØś ņĀüņĀĢ ĻĄ¼Ļ░äņØ┤ Ļ│ĀņĀäļźś ņ¬Įņ£╝ļĪ£ ņØ┤ļÅÖĒĢ£ļŗż.
4. ļäłĻ▓¤ ņ¦Ćļ”ä ņśłņĖĪ ļ¬©ļŹĖ Ļ░£ļ░£
4.1 ņŗ£ļ«¼ļĀłņØ┤ņģś ņĪ░Ļ▒┤
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæļČĆņØś ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆļŗż. ņØ╝ļ░śņĀü ņŗżĒŚśņØĆ ņĪ░Ļ▒┤ņŚÉ ļö░ļØ╝ ņØ┤ņé░(discrete)ņØś ņĪ░Ļ▒┤ņŚÉ ļīĆĒĢ£ Ļ▓░Ļ│╝ļź╝ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż
10). ĒĢśņ¦Ćļ¦ī ņśłņĖĪ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśļ®┤ ņŗżĒŚśņØä ĒĢśņ¦Ć ņĢŖĻ│ĀļÅä ņżæĻ░äĻ░ÆņŚÉ ļīĆĒĢ£ ņĀĢļ│┤ļź╝ ņ׳ņ¢┤ ņ£ĀņÜ®ĒĢśĻ▓ī ņé¼ņÜ®ĒĢĀ ņłś ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ņé¼ņÜ®ļÉ£ ļŹ░ņØ┤Ēä░ļŖö ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ĒåĄĒĢ£ 1500MPaĻĖē Ļ░Ģņ×¼ņØś ņĀĆĒĢŁ ņÜ®ņĀæ ĒŖ╣ņä▒ (I) -ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæņØś ļĪ£ļĖīĻ│ĪņäĀ ĒŖ╣ņä▒ ļČäņäØņØś ļŹ░ņØ┤Ēä░ļź╝ ĒÖ£ņÜ®ĒĢśņśĆļŗż.
ņÜ®ņĀæļČĆ ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ ĒÜīĻĘĆ ļČäņäØņØä ņé¼ņÜ®ĒĢśņŚ¼ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ĒÜīĻĘĆļ¬©ļŹĖņØĆ 1ņ░©, 2ņ░©, ļ╣äņäĀĒśĢļō▒ņØś ļŗżņ¢æĒĢ£ ļ¬©ļŹĖļĪ£ ĻĄ¼ņä▒ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ¤¼ļéś ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņé¼ņÜ®ļÉ£ ĒÜīĻĘĆļ¬©ļŹĖņØĆ ĒĢŁņØś Ļ│äņłśĻ░Ć 2ņ░©ņØĖ 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖ(second order polynomial regression model)ļĪ£ ņŗØņØĆ (3)ņÖĆ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ ╬▓ļŖö ĒÜīĻĘĆļ¬©ļŹĖņØś Ļ│äņłśņØ┤ļŗż. ĒÜīĻĘĆļ¬©ļŹĖņØś ņČ£ļĀźļ│ĆņłśļĪ£ ļäłĻ▓¤ ņ¦Ćļ”äņ£╝ļĪ£ ņŗØ (3)ņØś
y^ ļĪ£ ņĀĢņØśĒĢśņśĆĻ│Ā, ņ×ģļĀźļ│ĆņłśļĪ£ņŹ© ņÜ®ņĀæņĀäļźś, ņÜ®ņĀæņŗ£Ļ░ä, ņĀäĻĘ╣ Ļ░ĆņĢĢļĀź, 2Ļ░Ćņ¦Ć ņåīņ×¼ņØś Ļ░Ģņ×¼ņØś ņ×¼ņ¦ł, ļæÉ Ļ░Ģņ×¼ņżæņŚÉņä£ ņ¢ćņØĆ ĒīÉņ×¼ņØś ļæÉĻ╗śņÖĆ ļæÉĻ║╝ņÜ┤ ļæÉĻ║╝ņÜ┤ ĒīÉņ×¼ņØś ļæÉĻ╗śļź╝ Ļ░üĻ░ü
x1,
x2,
x3,
x4,
x5,
x6,
x7ņ£╝ļĪ£ ņĀĢņØśĒĢśņśĆļŗż. 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØś Ļ▓ĮņÜ░ ĒĢŁņØ┤ ņ┤Ø 36Ļ░£Ļ░Ć ļ░£ņāØĒĢśļ®░ ņØ┤ņŚÉ ļīĆĒĢ£ Ļ░ü ĒĢŁņØś Ļ│äņłśļŖö
Table 3Ļ│╝ Ļ░Öļŗż.
Table┬Ā3
Coefficient values for optimized 2nd order polynomial regression model
|
╬▓0
|
╬▓1
|
╬▓2
|
╬▓3
|
╬▓4
|
|
1.608 |
1.2815 |
0.0114 |
-0.01621 |
- |
|
╬▓5
|
╬▓6
|
╬▓7
|
╬▓11
|
╬▓12
|
|
0.0003 |
-1.9663 |
-0.5784 |
-0.10658 |
0.00305 |
|
╬▓13
|
╬▓14
|
╬▓15
|
╬▓16
|
╬▓17
|
|
0.00214 |
- |
-0.0001 |
0.23265 |
0.05289 |
|
╬▓22
|
╬▓23
|
╬▓24
|
╬▓25
|
╬▓26
|
|
-0.00217 |
0.00005 |
- |
-0.000001 |
0.0421 |
|
╬▓27
|
╬▓33
|
╬▓34
|
╬▓35
|
╬▓36
|
|
0.03563 |
-0.000004 |
- |
0.000002 |
-0.00109 |
|
╬▓37
|
╬▓44
|
╬▓45
|
╬▓46
|
╬▓47
|
|
-0.000789 |
- |
- |
- |
- |
|
╬▓55
|
╬▓56
|
╬▓57
|
╬▓66
|
╬▓67
|
|
-0.000005 |
- |
0.000255 |
- |
- |
|
╬▓77
|
|
|
|
|
|
- |
|
|
|
|
Table 3ņŚÉņä£ -ļŖö ļ¦żņÜ░ ņ×æņØĆ Ļ░ÆņØä ņØśļ»ĖĒĢ£ļŗż. Ēæ£ņÖĆ Ļ░ÖņØ┤ ņ×ģļĀźļÉśļŖö ļ¬©ļŹĖņØś ļ│ĆņłśĻ░Ć ļ¦ÄņĢäņ¦ÉņŚÉ ļö░ļØ╝ ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖņŚÉņä£ ĒĢŁņØś Ļ░£ņłśĻ░Ć ļ¦ÄņĢäņ¦ĆĻ│Ā ņØ┤Ļ▓āņØĆ Ļ│╝ļīĆ ņČöņĀĢ(overfitting)ņØś ļ¼ĖņĀ£ņĀÉņØä Ļ░¢ņØä ņłś ņ׳ļŗż. ļśÉĒĢ£ Ļ│äņłśĻ░ÆņØ┤ ļ¦żņÜ░ ņ×æņØĆ ļ│ĆņłśĻ░Ć ļéśĒāĆļéśļŖö ļ¼ĖņĀ£ņĀÉņØä Ļ░¢Ļ│Ā ņ׳ļŗż.
ņØ┤ļ¤¼ĒĢ£ ļ¼ĖņĀ£ņĀÉņØä Ļ│ĀļĀżĒĢśņŚ¼ ĒåĄĻ│äņĀüņ£╝ļĪ£ ņ£ĀņØśĒĢśņ¦Ć ņĢŖļŖö ĒĢŁņØś Ļ░£ņłśļź╝ ņżäņØ┤ĻĖ░ ņ£äĒĢśņŚ¼ ļ¬©ļōĀ ņäĀĒāØ, ņĀäņ¦äņäĀĒāØ, Ēøäļ░®ņĀ£Ļ▒░, ļŗ©Ļ│äļ│ä ĒÜīĻĘĆ ņżæ ļŗ©Ļ│äļ│ä ĒÜīĻĘĆ ĻĖ░ļ▓Ģ(stepwise regression)ņØä ņé¼ņÜ®ĒĢśņŚ¼ ĒÜīĻĘĆ ļ¬©ļŹĖņØś ĒĢŁņØś Ļ░£ņłśļź╝ ņĄ£ņĀüĒÖö ĒĢśņśĆļŗż,
ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ│ĆņłśņäĀĒāØ ļ░®ļ▓ĢņØĆ ņŗ£ļ«¼ļĀłņØ┤ņģś ņĪ░Ļ▒┤Ļ│╝ ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ļź╝ ļŗ©Ļ│äļ│ä ĒÜīĻĘĆļź╝ ĒåĄĒĢ┤ ĒÜīĻĘĆ ļ¬©ļŹĖņØä ņĢäļל ņŗØ(4)Ļ│╝ ļéśĒāĆļé┤ņŚłļŗż.
ņŚ¼ĻĖ░ņä£ ╬▓ļŖö ņĄ£ņĀüĒÖöļÉ£ ĒÜīĻĘĆļ¬©ļŹĖņØś Ļ│äņłśņØ┤ļ®░ Ļ░ü ņ×ģļĀźļ│ĆņłśņØś ņ▓©ņ×ÉņÖĆ Ļ░Öļŗż. ĒÜīĻĘĆ ļ¬©ļŹĖņØś Ļ│äņłśļŖö ņĄ£ņåīņĀ£Ļ│▒ļ▓Ģ(least square method)ņ£╝ļĪ£ ĻĄ¼ĒĢśņŚ¼ ņśżņ░©ņØś ņĀ£Ļ│▒ņØä ņĄ£ņåīĒÖö ĒĢĀ ņłś ņ׳ļÅäļĪØ ĒĢśņśĆļŗż. ļ¬©ļŹĖņŚÉ ļīĆĒĢ£ Ļ│äņłśļŖö
Table 4ņÖĆ Ļ░Öļŗż.
Table┬Ā4
Coefficient values for optimized 2 order polynomial regression model
|
╬▓0
|
╬▓1
|
╬▓2
|
╬▓3
|
|
-0.35181 |
-0.01708 |
0.0021 |
0.00104 |
|
╬▓4
|
╬▓5
|
╬▓6
|
|
|
0.00002 |
0.0201 |
-0.1074 |
|
4.2 ĒÜīĻĘĆļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖź
Ļ░ü ĒÜīĻĘĆļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖź ĒÅēĻ░Ćļź╝ ņ£äĒĢ┤ ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ļĪ£ ņ¢╗ņØĆ ņÜ®ņĀæļČĆ ļäłĻ▓¤ ņ¦Ćļ”äĻ│╝ ĒÜīĻĘĆļ¬©ļŹĖļĪ£ ņ¢╗ņØĆ ļäłĻ▓¤ ņ¦Ćļ”äņØś ņśłņĖĪ Ļ░ÆņØś ņāüĻ┤Ćņä▒ņØä ĻĘĖļלĒöäļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ļéśĒāĆļé┤ņŚłļŗż.
Fig. 4ņÖĆ 5ļŖö Ļ░üĻ░ü 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖĻ│╝, ņĄ£ņĀüĒÖöļÉ£ 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆ ļ¬©ļŹĖņØś ļ╣äĻĄÉ ĻĘĖļלĒöäņØ┤ļŗż. ĻĘĖļ”╝ņØä ĒåĄĒĢ┤ 2ņ░© ļ¬©ļŹĖņØś Ļ▓ĮņÜ░ ļæÉ Ļ░£ ļ¬©ļæÉ ņĀäņ▓┤ņĀüņ£╝ļĪ£ ņśłņĖĪņä▒ļŖźņØ┤ ļ╣äņŖĘĒĢ£ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż.
Fig.┬Ā4
Nugget diameter comparison between simulation values and estimated values for 2nd order polynomial model
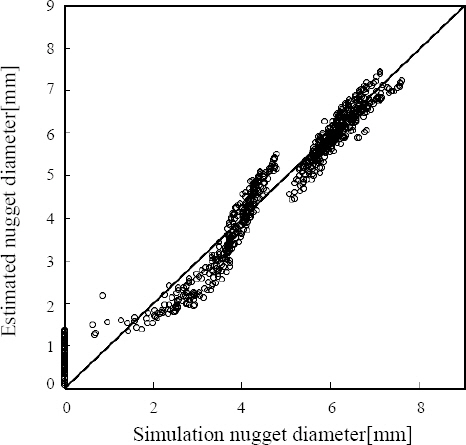
ļæÉ ļ¬©ļŹĖ ļŗż ņŗ£ļ«¼ļĀłņØ┤ņģś ņØś ļäłĻ▓¤ ņ¦Ćļ”äņØ┤ 0ņØĖ Ļ▓ĮņÜ░ ņśżņ░©Ļ░Ć Ēü¼Ļ▓ī ļÉśļŖöļŹ░, ņØ┤Ļ▓āņØĆ ļ¬©ļōĀ ņ×ģļĀźĻ░ÆņØ┤ 0ņØ┤ ļÉśņ¢┤ņĢ╝ ĒÜīĻĘĆ ļ¬©ļŹĖņØś Ļ░ÆņØ┤ 0ņØ┤ ļÉśĻĖ░ ļĢīļ¼ĖņØ┤ļ®░ ĒÜīĻĘĆļ¬©ļŹĖņØś ĒĢ£Ļ│äņĀüņØĖ ļČĆļČäņØ┤ļØ╝Ļ│Ā ĒĢĀ ņłś ņ׳ļŗż. ņĄ£ņĀüĒÖöļÉ£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØś Ļ▓ĮņÜ░ ļ│ĆņłśĻ░Ć ņĀüņØīņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖĻ│╝ ņśłņĖĪ ņä▒ļŖźņØ┤ ļ╣äņŖĘĒĢ£ Ļ▓āņØä ņĢī ņłś ņ׳ņŚłļŗż.
ĒÜīĻĘĆļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØś ņĀĢļץņĀü ĒÅēĻ░ĆļĪ£ļŖö ņāüĻ┤ĆĻ│äņłś, Ļ▓░ņĀĢĻ│äņłś, F-Ļ▓Ćņ”Ø, ĒÅēĻĘĀ ņśżņ░©ņ£© ļō▒ ļŗżņ¢æĒĢ£ ļ░®ļ▓Ģņ£╝ļĪ£ ņłśĒ¢ēļÉśņ¢┤ņ¦äļŗż
4). ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Ļ░üĻ░üņØś ļ¬©ļŹĖņŚÉ ļīĆĒĢ£ Ļ▓░ņĀĢ Ļ│äņłś(coefficient of determination:
R2)ņÖĆ ĒÅēĻĘĀ ņśżņ░©ņ£©(average error rate: AER)ņØä ņé¼ņÜ®ĒĢśņŚ¼ ļ¬©ļŹĖņŚÉ ļīĆĒĢ£ ņśłņĖĪ ņä▒ļŖźņØä ĒÅēĻ░ĆĒĢśņśĆļŗż. ĒÅēĻĘĀ ņśżņ░©ņ£©Ļ│╝ Ļ▓░ņĀĢĻ│äņłśņØś ņŗØņØĆ Ļ░üĻ░ü ņĢäļלņØś ņŗØ (5)ņÖĆ (6)Ļ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£
R2 ļŖö Ļ▓░ņĀĢĻ│äņłśņØ┤Ļ│Ā,
i ļŖö ļŹ░ņØ┤Ēä░ ļ▓łĒśĖ,
n ņØĆ ļŹ░ņØ┤Ēä░ņØś ņ┤Ø Ļ░£ņłśņØ┤ļŗż.
y ļŖö ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ņØś ņØĖņןņĀäļŗ©Ļ░ĢļÅä,
y┬» ļŖö
y ņØś ĒÅēĻĘĀĻ░Æ,
y^ ļŖö ņśłņĖĪļ¬©ļŹĖņŚÉ ņØśĒĢ┤ Ļ│äņé░ļÉ£ Ļ░Æ,
y^┬» ļŖö
y^ ņØś ĒÅēĻĘĀĻ░ÆņØ┤ļŗż. ņŗØ (5)ņÖĆ ņŗØ (6)ļź╝ ĒåĄĒĢśņŚ¼ Ļ░ü ļ¬©ļŹĖņŚÉ ļīĆĒĢ£ Ļ▓░ņĀĢĻ│äņłś ļ░Å ĒÅēĻĘĀ ņśżņ░©ņ£©ņØä ĻĄ¼Ē¢łņ£╝ļ®░
Table 5ņŚÉ Ļ░ü ļ¬©ļŹĖņŚÉ ļīĆĒĢśņŚ¼ ļ╣äĻĄÉĒĢśņśĆļŗż. Ļ▓░ņĀĢĻ│äņłśļŖö 1ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ņśłņĖĪ ņä▒ļŖźņØ┤ ņÜ░ņłśĒĢśĻ│Ā, ĒÅēĻĘĀ ņśżņ░©ņ£©ņØĆ 0ņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ĒÜīĻĘĆļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØ┤ ņÜ░ņłśĒĢśļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż. Ēæ£ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ Ļ▓░ņĀĢĻ│äņłśņŚÉņä£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØ┤ ļ»ĖņäĖĒĢśĻ▓ī ņĪ░ĻĖł ļŹö ņÜ░ņłśĒĢ£ ņśłņĖĪ ņä▒ļŖźņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ņØīņØä ņĢī ņłś ņ׳ņŚłļŗż. ĒĢśņ¦Ćļ¦ī ņĄ£ņĀüĒÖöļÉ£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖ ļśÉĒĢ£ ņĀüņØĆ ļ│ĆņłśļĪ£ Ļ▒░ņØś ņ£Āņé¼ĒĢ£ ņśłņĖĪ ņä▒ļŖźņØä Ļ░Ćņ¦ĆļŖö Ļ▓āņØä ĒÖĢņØĖ ĒĢĀ ņłś ņ׳ņŚłļŗż. ņĄ£ņĀüĒÖöļÉ£ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņØś Ļ▓ĮņÜ░ ĻĖ░ņĪ┤ 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖņŚÉņä£ ļ¦ÄņØĆ ņ×ģļĀźņØĖņ×ÉļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢĀ ņłś ņ׳ļŖö Ļ│╝ļīĆ ņČöņĀĢņØä ļ░®ņ¦ĆĒĢśļ®┤ņä£, 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖĻ│╝ Ļ▒░ņØś ļ╣äņŖĘĒĢ£ ņśłņĖĪņä▒ļŖźņØä Ļ░Ćņ¦ĆļŖö Ļ▓āņØä ņĢī ņłś ņ׳ņŚłļŗż. ĻĘĖ Ļ▓░Ļ│╝ ļæÉ ļ¬©ļŹĖ ļ¬©ļæÉ ņÜ░ņłśĒĢ£ ņśłņĖĪņä▒ļŖźņØä Ļ░¢Ļ│Ā ņ׳ņØīņØä ĒÖĢņØĖ ĒĢśņśĆļŗż.
Table┬Ā5
Coefficient of determination and average error rate for regression model
|
Regression model |
R2
|
AER |
|
2nd order |
0.955 |
0.169 |
|
Optimized 2nd order |
0.951 |
0.169 |
5. Ļ▓░ ļĪĀ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö 1500MPaĻĖē ĒĢ½ņŖżĒā¼ĒĢæĻ░ĢņŚÉ ļīĆĒĢ┤ ļÅÖņóģņ×¼ļŻī, ņØ┤ņóģņ×¼ļŻī, ļÅÖņóģļæÉĻ╗ś, ņØ┤ņóģļæÉĻ╗śņŚÉ ļīĆĒĢ£ ņĀĆĒĢŁ ņĀÉ ņÜ®ņĀæ ĒŖ╣ņä▒ņØä ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņłśĒ¢ēĒĢśņśĆĻ│Ā ņÜ®ņĀæļČĆņØś ļäłĻ▓¤ņØś ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆļŗż.
1) FEM ņŗ£ļ«¼ļĀłņØ┤ņģśņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĒĢ½ņŖżĒā¼ĒĢæĻ░ĢņØś ļæÉĻ╗ś 1.0mmņÖĆ 1.4mmņØś ļÅÖņóģ Ļ░ĢĒīÉĻ│╝ 1.0mmņÖĆ 1.4mmņØś ņØ┤ņóģ ļæÉĻ╗ś Ļ░ĢĒīÉņŚÉ ļīĆĒĢśņŚ¼ ļĪ£ļĖīĻ│ĪņäĀ ņĀ£ņĢłĒĢśņśĆļŗż.
2) ņŗ£ļ«¼ļĀłņØ┤ņģś Ļ▓░Ļ│╝ļź╝ ĻĘ╝Ļ▒░ļĪ£ ĒĢśņŚ¼ ņÜ®ņĀæļČĆņØś ļäłĻ▓¤ ņ¦Ćļ”äņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļÅäļĪØ ņÜ®ņĀæņĀäļźś, ņÜ®ņĀæņŗ£Ļ░ä, ņĀäĻĘ╣ Ļ░ĆņĢĢļĀź, 2Ļ░Ćņ¦Ć ņåīņ×¼ņØś Ļ░Ģņ×¼ņØś ņ×¼ņ¦ł, ļæÉ Ļ░Ģņ×¼ņØś ļæÉĻ╗śļź╝ ņ×ģļĀźņØĖņ×ÉļĪ£ ĒĢśļŖö 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆ ļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆļŗż.
3) ļ¦ÄņØĆ ņ×ģļĀź ņØĖņ×ÉļĪ£ ļČĆĒä░ ļŗ©Ļ│äļ│ä ĒÜīĻĘĆ ĻĖ░ļ▓Ģ(stepwise regression)ņØä ļÅäņ×ģĒĢśņŚ¼ ņĄ£ņĀüĒÖöļÉ£ 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖņØä ņĀ£ņĢłĒĢĀ ņłś ņ׳ņŚłļŗż.
Fig.┬Ā5
Nugget diameter comparison between simulation values and estimated values for optimized 2nd order polynomial model
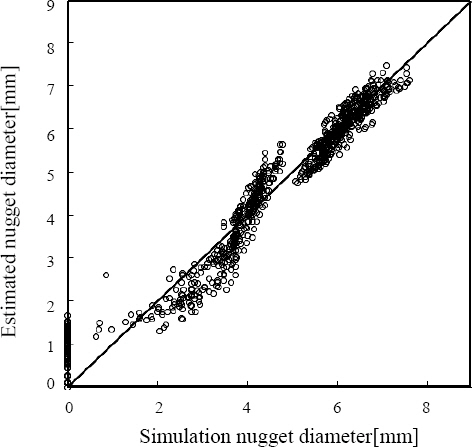
4) 2ņ░© ĒÜīĻĘĆļ¬©ļŹĖĻ│╝ ņĄ£ņĀüĒÖö ļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØä Ļ▓░ņĀĢ Ļ│äņłśņÖĆ ĒÅēĻĘĀ ņśżņ░©ņ£©ļĪ£ ĒÅēĻ░ĆĒĢśņśĆņ£╝ļ®░ Ļ▓░ņĀĢĻ│äņłśļŖö Ļ░üĻ░ü 0.955, 0.951 ņØ┤ļ®░, ĒÅēĻĘĀņśżņ░©ņ£©ņØĆ ļ¬©ļæÉ 0.169ņśĆņ£╝ļ®░, ĻĘĖ Ļ▓░Ļ│╝ ļæÉ ļ¬©ļŹĖ ļ¬©ļæÉ ļ╣äņŖĘĒĢ£ ņśłņĖĪņä▒ļŖźņØä Ļ░¢Ļ│Ā ņ׳ņØīņØä ĒÖĢņØĖ ĒĢĀ ņłś ņ׳ņŚłļŗż.
Acknowledgments
ņØ┤ ļģ╝ļ¼ĖņØĆ 2014ĒĢÖļģäļÅä ļČĆĻ▓ĮļīĆĒĢÖĻĄÉ ņŚ░ĻĄ¼ļģä[II] ĻĄÉņłś ņ¦ĆņøÉņé¼ņŚģņŚÉ ņØśĒĢśņŚ¼ ņŚ░ĻĄ¼ļÉśņŚłņØī (C-D-2014-0716)
References
4. C. Son and Y. W. Park, Strength Estimation Model of Resistance Spot Welding in 780MPa Steel Sheet Using Simulation for High Efficiency Car Bodies,
Journal of the Korean Society for Power System Engineering. 19(2) (2015) 70ŌĆō77.
https://doi.org/10.9726/kspse.2015.19.2.070
[CROSSREF] [PDF] 5. C. M. Calva and T. W. Eagar, Enhancement of the Weldability in Resistance Spot Welding, AWS Detroit Section, Sheet Metal Welding Conference IV. (1990)
6. T. M. Hong, Y. B. Choi, S. P. Kim, J. H. Lee, and H. S. Chang, Estimation of Nugget Size Using Artificial Neural Network &Comparison to Regression Method for Re-sistance Spot Welding, Proceedings of KSME Spring Conference. 1(1) (1993) 929ŌĆō932.
7. C. V. Nielsen, W. Zhang, L. M. Alves, N. Bay, and P.A.F. Martins, Modeling of Thermo-Electro-Mechanical Manufacturing Processes with Applications in Metal Forming and Resistance Welding, Springer. (2012) 19ŌĆō27.
8. S. Y. Lee, T. H. Ko, W. H. Kee, and Y. H. Jang, Weld-ability Evaluation of Resistance Spot Welding using CAE Methodology, Journal of the 30th anniversary of the Korean Society of Automotive Engineers. 3 (2008) 1351ŌĆō1356.
9. T. H. Kim, D. O. Lee, and S. Rhee, Development of Resistance Spot Weldability Estimation Using Lobe Diagram for Steel Plate of Automobiles, Journal of KWJS. 23(4) (2005) 59ŌĆō65.









 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print