머신러닝을 이용한 레이저 용접부의 모델링 Part I: Al/Cu 이종재료 겹치기 레이저용접부의 용입깊이
Modeling of Laser Welds Using Machine Learning Algorithm Part I: Penetration Depth for Laser Overlap Al/Cu Dissimilar Metal Welds
Article information
Abstract
Thin sheets of Al/Cu dissimilar materials are overlap welded for the electrical connection of secondary battery electrodes by laser welding. The weld penetration depth is an important joint quality to ensure strength and electrical conductance. It is difficult to predict the penetration depth using analytical methods because of the high laser reflection and small thickness of the base materials. Several machine learning algorithms were investigated to develop regression models for the penetration depth. The models included linear regression, decision tree, supported vector regression, Gaussian process regression, and decision tree ensemble model groups. The regression models with high degrees of freedom showed excellent mean absolute percentage errors (MAPE) and coefficients of determination (R2). In particular, the Gaussian process regression model with exponential kernels had an MAPE of 0.2% and an R2 of unity.
1. 서 론
아크 용접이나 레이저용접과 같이 외부열원을 이용하는 용융용접에서의 용접품질을 예측하기 위해 온도분포에 대한 다양한 모델링을 적용하고 있다. 열전도 지배방정식을 풀기 위해 로젠탈 식을 대표적으로 하는 해석 모델(analytic model)과 유한요소나 유한체적/차분을 이용한 수치 모델(numerical model) 등을 채용하여 용접부의 온도분포를 구할 수 있고, 이를 기반으로 용접부의 크기, 용접비드의 폭이나 깊이를 예측할 수 있다1). 저항용접의 주요 열원이 소재내부의 저항 및 접촉저항임에 비해 아크용접이나 레이저용접에서는 외부열원이 용융을 일으키므로 외부열원과 용접부의 상호작용의 모델링이 온도분포해석의 가장 중요한 부분이다. 기존에는 Goldak 모델2)과 같은 이중열원 모델이 많이 채택되었는데, 아크 압력에 의한 용융풀 표면의 형성3), 용융풀 표면에서의 아크/플라즈마에 의한 에너지 흡수와 용융풀 안쪽에서의 용적의 침투로 인한 에너지 흡수4-6), 키홀 내부에서는 다중반사로 인한 에너지 흡수7-9) 등이 고려되었다.
종횡비가 큰 레이저 용접에서 키홀과 용입의 깊이는 용접부의 품질을 결정하는 중요한 요소이고, 레이저 출력, 용접속도, 레이저 빔의 크기, 빔 품질 등이 용입을 결정하는 변수로 실험적으로 규명되었다10-12). 이론적, 실험적 근거하에 지배방정식을 풀지 않고 레이저 용접 공정변수로부터 용입을 예측하기 위해 다양한 인덱스 개발하려는 연구가 계속되고 있다. 레이저용접에서 레이저와 소재사이의 상호작용인자는 소재 표면에서의 레이저 에너지밀도(q)와 상호작용시간(t)이라고 알려져 있었다. 여기에서 레이저 에너지밀도는 레이저 에너지(P)를 소재 표면에서 빔의 면적(A)으로 나눈 인덱스이며(q=P/A), 상호작용 시간은 레이저 빔의 직경(d)을 용접속도(V)로 나눈 인덱스이다(t=d/V). Dausinger et al.은 알루미늄과 철강의 레이저용접에서 레이저 출력(P)과 초점에서의 빔직경(d)의 비(P/d)가 깊은 용입을 만드는 기준이라고 실험적으로 규명하였다13). Suder et al.의 연구에서도 출력과 빔직경의 비(P/d)를 파워팩터(power factor)로 정의하고 상호작용시간과 파워팩터가 용입을 결정하는 것을 확인하였다14). Suder et al.의 다른 연구15)에서는 또 다른 레이저와 소재사이의 상호작용 인자로 용접선위의 한 점에서 받는 총 에너지를 특정포인트 에너지(specific point energy)를 정의하였고, 이는 레이저출력과 상호작용시간의 곱으로 정의하였다. Coroado et al.과 Zavala-Arredondo et al.16)의 연구에서도 파워팩터, 상호작용시간, 특정포인트 에너지를 인덱스로 하여 레이저 용융현상을 설명하고자 하였다. Kim and Ki는 레이저용접에서 레이저에너지 밀도, 상호작용 시간, 키홀내 다중반사강도를 조합하여 인덱스를 개발하고 전도모드와 키홀모드의 레이저 용접에서 용입예측에 이용하였다17). Fabbro et al.은 레이저 에너지(P), 빔 직경(d), 용접속도(V)에 기반한 인덱스를 이용하여 키홀의 종횡비를 예측하였다18). Fabbro는 다른 논문 19)에서 이 3개의 공정변수와 열전도도, 밀도, 비열을 소재 변수로 이용하여 레이저용접과 SLM(Selective Laser Melting)공정에서 일반화된 스케일링 법칙을 적용할 수 있음을 제안하였다.
지배방정식이나 물리적 인덱스를 기반한 접근과 달리 최근에는 데이터에 기반한 기계학습(Machine learning)을 용접문제에 적용하려는 연구도 활발하다. 기계학습의 경우 물리적 법칙에 기반하지 않고 주어진 데이터에 기반하여 법칙을 스스로 도출하는 학습방법으로 딥러닝으로 많이 알려진 신경회로망이 가장 대표적인 알고리즘이며, 비신경회로망으로 서포트 벡터머신(SVM, Supported Vector Machine), 랜덤포레스트(Random Forrest), GBT(Gradient Boosted Trees) 등의 고전적 접근방법도 최근에 다시 주목을 받고 있다. 저자들은 선행논문20,21)에서 영상에 기반한 딥러닝을 용접부문에 적용한 사례에 대해 소개하였으며, 본 연구에서는 Al/Cu 이종재료 레이저용접부의 용입예측에 기계학습을 적용한 결과를 소개하고자 한다.
2. 데이터 수집 및 모델링방법
2.1 데이터의 수집
본 연구에서는 Leitz의 논문22)에 공개된 Al/Cu 이종재료 용접부에 대한 데이터를 이용하였다. 실험에 사용된 재료는 탈산동(Cu-PHC)과 Al 1050합금으로 탈산동의 경우 두께 0.3 mm, 1 mm의 박판을 사용하고, Al 합금의 경우 두께 0.5 mm, 1 mm의 박판을 사용하였다. 겹치기 용접부에서 0.3 mm 탈산동/ 0.5 mm Al 1080 두께 조합과 각 소재 1 mm 두께 조합이 사용되었으며, 상하배치를 바꾸어서 총 4개의 조합을 만들었다.
실험에 사용한 레이저는 싱글모드 파이버 레이저(1070 nm 파장)와 멀티모드 디스크레이저(1034 nm 파장)가 이용되었는데 파이버레이저의 경우 14 µm, 50 µm 직경의 파이버로 전송하여 용접부에서 20 µm, 83 µm 직경의 레이저 빔 직경을 형성하였다. 디스크레이저 100 µm, 200 µm 직경의 파이버로 전송하여 용접부에 170 µm, 200 µm, 340 µm 직경의 레이저 빔 직경을 형성하였다.
각 소재 조합별로 다른 레이저 출력이 적용되었으며, 적용된 레이저 출력의 범위는 700 W에서 5 kW이다. 용접속도는 1 m/min에서 40 m/Min 범위에서 조정되었다.
조건별로 최소 2개 이상의 단면 시편을 촬영하여 용입깊이를 측정하였으며, 논문의 데이터를 기반으로 본 연구에서는 250개의 조건에 대한 용입데이터를 수집하였다.
2.2 머신러닝 모델
본 연구에서는 수집된 데이터를 MATLAB® R2019a 버젼의 통계/기계학습 툴박스(Statistics and Machine Learning Toolbox™)의 회귀프로그램을 이용하여 기계학습하였다23). 사용한 회귀 학습 모델은 크게 선형회귀(linear regression), 의사결정 트리(decision tree), SVM, 가우스 프로세스 회귀(GPR, Gauss Process Re- gression), 회귀트리 앙상블 (Decision tree ensemble) 모델로 각각의 특징은 아래와 같다.
2.2.1 선형회귀모델
먼저 선형회귀 모델은 독립변수와 종속변수가 선형 관계임을 가정하고 종속변수의 값을 예측하는 회귀 모델이다. 일반적인 n개 변수에 대한 다변량 선형회귀 모델은 식(1)과 같다.
여기에서 Y는 종속변수, βk는 k번째 계수(β0는 상수항), X는 독립변수, ε은 오차항이다.
이를 확장하여 일반화된 선형회귀모델을 만들면 식 (2)와 같다.
여기에서 fi는 독립변수들을 인자로 하는 스칼라 함수로 비선형 및 다항식을 포함한다. 선형회귀 함수는 비교적 단순한 형태이며, 선형이 아닌 시스템에서는 성능이 낮을 수 있다. 본 논문에서는 선형회귀 모델을 총 네 가지 방법(선형, 상호 작용 선형, 강건 선형 및 단계적 선형)으로 학습하였다. 선형과 상호작용 선형 회귀의 경우 최소자승오차를 이용하여 회귀모델을 도출하는 방법이다. 강건(robust) 선형회귀는 선형회귀에서 데이터를 왜곡시키는 극단치(outlier)의 효과를 줄이기 위해 사용되는 방법으로 가중치를 조정하는 방법이다. 단계적 선형회귀의 경우 모든 항을 넣지 않고 성능이 더 이상 향상되지 않을 때까지만 단계적으로 항을 추가하여 최적화를 하는 방식이다.
2.2.2 의사결정트리
의사결정 트리는 다단계(multistage) 의사결정 알고리즘의 하나로 복잡한 의사결정 과정을 단순한 여러 개의 의사결정의 조합으로 구성하여 최종적인 종속변수 예측이 가능한 알고리즘으로24), 회귀 및 분류에 모두 사용되는 비모수(non-parametric) 모델의 일종이다. 데이터 세트를 특정한 기준을 가지고 분기점을 만들어 나가며 결과를 매칭하는 방법으로 분기점에 의해 나뉘어진 전체적인 모델의 형상이 나무와 같아 의사결정 트리라 한다. 이러한 분기점 및 분기점에 의해 나눠진 새로운 끝단을 모두 노드(node)라 부르고, 최종 결정 노드를 잎(leaf) 노드라 한다. 분류 문제에서 결정트리의 적합성은 노드내에 속한 데이터들의 불순도(impurity)로 평가하며, 이를 정량화하기 위해 식 (3)과 같은 엔트로피(entropy) 함수, H가 사용된다24).
pi는 노드 내에 i번째 클래스에 속한 데이터 개수의 비율이다. 예를 들어 해당 노드에 클래스 1이 2개, 클래스 2가 8개 존재할 경우 p1=0.2, p2=0.8이다. 각 노드의 엔트로피가 낮을수록 순도가 높고, 엔트로피가 높을수록 불순도가 높아 의사결정 트리는 엔트로피가 낮아지는 방향으로 학습을 진행한다. 본 연구에서 적용한 회귀문제에서는 평균 제곱오차(Mean Square Error)가 낮아지는 방향으로 학습을 한다23). 분기점이 많을수록, 즉, 가지가 많을수록 모델의 성능이 향상되나 과적합이 일어날 수 있다. 학습에는 세 가지 종류(성긴 트리, 중간 트리 및 조밀 트리)의 의사결정 트리모델을 사용하였는데 각각의 트리는 분기된 잎노드에 연결된 데이터의 개수가 각각 36, 12, 4개 이하일 때까지 학습을 한다.
2.2.3 SVM
SVM은 이진분류 문제를 풀기 위해 고안된 알고리즘으로 데이터를 최대 마진으로 분류할 수 있는 초평면을 찾는 알고리즘이다25). SVM은 일반화 특성이 우수하여 회귀 문제에도 적용이 가능하다. 본 연구에서 적용한 알고리즘은 ε-여유 혹은 ε-튜브 (epsilon-insensitive) SVM으로 오차가 ±ε내에 있을 경우에는 손실함수가 0이 되도록 손실함수를 정의한다. 비선형함수의 경우에는 고차원 공간으로 데이터를 매핑한 후 초평면을 찾을 수 있으며, 이 때 비선형성을 가진 커널 함수(kernel function)을 채택한다. 학습에는 여섯 종류(선형, 2 차, 3 차, 성긴 가우스, 중간 가우스 및 조밀 가우스 SVM)의 커널을 채택된 SVM모델을 사용하였으며, 사용된 커널 함수는 Table 1과 같다. Table 1에서 xj, xk는 독립변수의 쌍이며, 가우시안 커널에서 데이터를 나누는 단위를 커널스케일(kernel scale)이라고 하는데 독립변수의 개수가 P인 경우 성긴, 중간, 조밀 가우스 SVM에서는 커널 스케일이 각각 4√P, √P, √P/4이다23).
2.2.4 회귀트리 앙상블
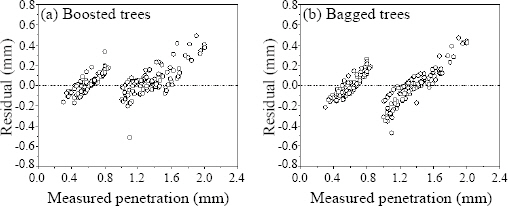
회귀트리 앙상블은 강력한 모델을 만들기 위해 여러 의사결정 트리를 연결하는 기법으로 본 연구에서는 배깅(Bagging, Bootstrap Aggregating)과 부스팅(Boosting)이 사용되었다23,26). 배깅에서는 입력데이터로부터 복원추출한 여러 개의 샘플세트를 이용하여 회귀트리를 학습하고, 학습된 모델의 결과를 집계하는 방식으로 최종 결정을 내리는 방법으로, 배깅기법 중 각 모델별로 랜덤한 종속변수 세트가 정해질 경우 램덤 포레스트라 부른다. 부스팅은 의사결정 트리를 이용해 학습한 결과에서 틀린 결과에 대해 높은 가중치를 두고 다시 학습을 반복하는 방법이다. 회귀트리 앙상블은 두 종류(배깅 트리, 부스팅 트리)를 사용하였다.
2.2.5 가우스 프로세스 회귀 (GPR)
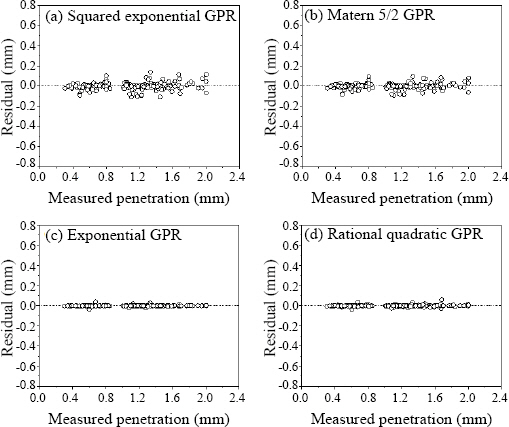
GPR은 가우스 프로세스를 이용하여 회귀를 모델링하는 기법으로 제곱지수(squared exponential), 메이턴 5/2(Matern 5/2), 지수(exponential) GPR, 유리 2차(rational quadratic) GPR이 이용되었다. 가우스 프로세스에서는 평균함수와 공분산(covariance)함수를 이용해서 회귀함수에 대한 분포를 정의하는데 공분산 함수는 커널함수라고도 불리면 Table 2와 같이 다양한 함수가 사용된다. 커널 파라미터에는 표준 편차 σf가 포함되어 있고, σl은 입력값의 거리를 나타내는 특징 길이이다. r은
3. 결과 및 토론
3.1 회귀결과
레이저 용접 용입 깊이를 예측하기 위해 6개의 변수(배열, 상판 두께, 하판 두께, 용접 속도, 레이저 출력 및 지름)을 사용하여 회귀 분석을 실시하였다. 실험에는 앞 절에서 서술한 총 19 가지 회귀 모델을 사용하여 회귀 분석을 하였다.
본 논문에서 회귀 모델의 평가는 절대 평균 오차율(Mean Absolute Percentage Error, MAPE)와 결정 계수(R2)를 통해 나타냈다. 절대 평균 오차율은 각각의 예측값과 절대값 오차의 비의 평균을 나타내며 식(4)와 같다.
여기에서 n은 총 데이터의 개수, y(i)와 y’(i)는 각각 i번째 데이터의 실제값과 예측값이다.
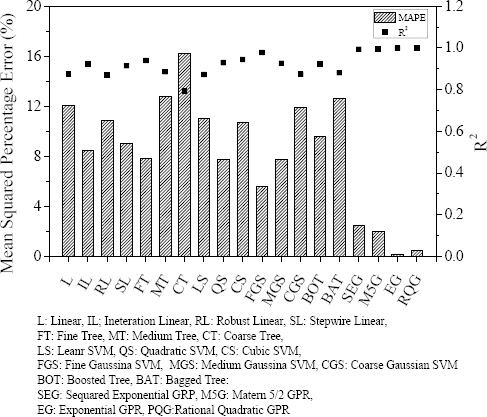
각 모델의 절대 평균 오차율과 결정계수를 Fig. 1에 나타내었다. 절대 평균 오차율과 결정 계수에 함께 절대 평균 오차(Mean Absolute Error, MAE)를 Table 3에 나타내었다.
모델의 확장성이 높은 GPR의 경우 가장 작은 오차율과 높은 결정계수를 가지고 있었으며, 거의 완벽하게 예측이 가능하다. 모델 중에서는 성긴 트리에서 가장 높은 오차율과 낮은 결정계수가 확인되었다. 성긴 트리에서는 마지막 잎노드에 포함된 데이터의 개수가 36개 이하이면 모델 최적화를 중단하는데 전체 데이터 개수가 250개이므로 너무 단순화된 모델이기 때문으로 판단된다.
각 모델링 기법에서는 모델의 차원이 높을수록 작은 오차율과 높은 결정계수를 가진다. 즉, 의사결정트리 모델에서는 분기가 많아 잎노트의 개수가 작은 조밀트리가 오차가 작은 모델이었으며, 가우시안 SVM에서도 조밀 가우시안 SVM이 가장 오차가 작은 모델이었다.
3.2 잔차 분석
각 회귀 모델의 유의성 및 잔차 경향을 검정하기 위한 잔차분석을 실시하였다. 이상적인 경우 모델은 낮은 오차율과 무작위 분포 및 등분산의 잔차를 가진다.
3.2.1 선형회귀 모델
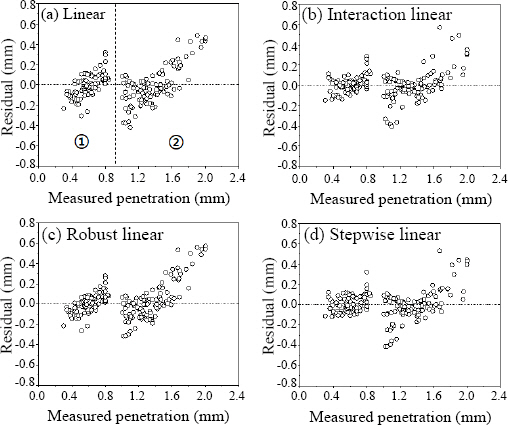
선형회귀 모델의 잔차 그래프를 Fig. 2에 나타내었다. 그래프에서 잔차는 측정값 900 µm를 기준으로 두 그룹으로 나누어지는 모습을 보인다. 이러한 분리는 소재 두께 조합에 따라 나타난다. Fig. 2의 ①그룹은 Al 0.5 mm/Cu 0.3 mm의 조합이며, 0.8 mm에서 완전 용입을 가진다. Fig. 2의 ②그룹은 Al 1 mm/Cu 1 mm의 조합이며 2 mm에서 완전 용입을 가진다.
선형회귀 모델은 다른 회귀 모델에 비교하여 비교적 높은 절대 평균 오차율과 낮은 결정 계수를 보였는데 (Table 3), 잔차분석 결과 잔차가 무작위로 분포하지 않고 우상향으로 경향성을 보이고 있는 모습을 확인할 수 있다. 즉, 선형모델로는 용입 깊이 예측 회귀가 어려우며 잔차가 아치형의 분포도 아니므로 2차 회귀모델보다 높은 차수의 회귀 모델의 적용이 필요함을 확인하였다.
3.2.2 의사결정트리 회귀모델
의사 결정 트리 모델의 잔차 분석 결과를 Fig. 3에 나타내었다. 잔차분석 결과 최소잎노드의 크기가 작은 조밀 모델의 경우 정확도가 높이지고 잔차의 경향성이 줄어드는 모습을 확인할 수 있었으나, 선형회귀와 마찬가지로 우상향으로 향하는 경향성이 확인되었다.
3.2.3 SVM 회귀 모델
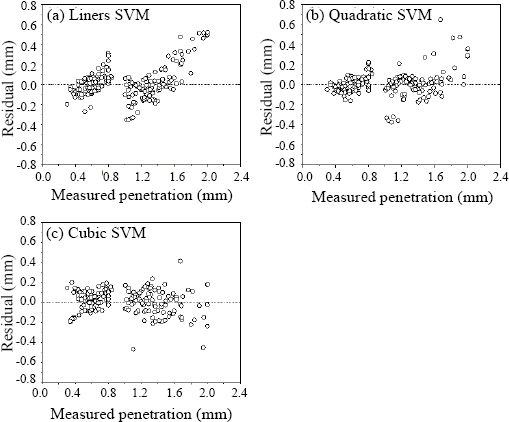
SVM 회귀 모델에서는 선형, 2차 및 3차 회귀 모델(Fig. 4)과 가우시안 커널(Fig. 5)을 적용한 회귀 모델을 사용하였다.
다항식 커널을 이용한 SVM 회귀 모델의 경우 커널의 차수가 높아질수록 잔차의 경향성이 옅어지며 점차 무작위로 분포되는 모습을 확인할 수 있었다. 2차에서 3차함수로 커널의 차수가 커지는 경우에는 예상외로 절대 표준 오차율과 결정계수가 동시에 커지는 높아지는 현상이 있었는데(Table 3), 3차함수를 커널로 사용할 경우 잔차의 경향이 무작위로 변하지만 표준편가가 증가하기 때문으로 확인되었다 (Fig. 4).
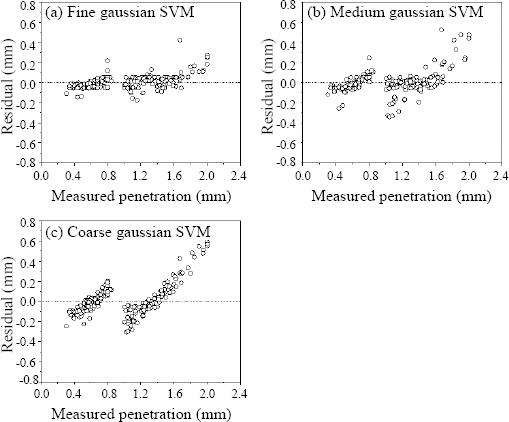
마찬가지로 가우시안 커널을 적용한 SVM은 커널스케일이 작을수록 잔차의 경향성이 줄어들었으며 잔차의 크기도 줄어드는 모습을 확인할 수 있었다(Fig. 5). 가우시안 커널을 사용할 경우 데이터셋을 무한대 차원으로 매핑할 수 있어 커널 스케일을 작게할 경우 충분한 비선형 회귀를 구현할 수 있다. 또한, 가우시안 SVM을 적용했음에도 낮은 커널 스케일에서는 잔차가 경향성을 가지고 있어 독립변수들과 용입 깊이 사이에 강한 비선형성이 있음을 확인할 수 있다.
3.2.4 회귀트리 앙상블 회귀모델
회귀트리 앙상블의 경우 일반적인 의사결정 트리와 비교하여 부스팅 트리와, 배깅 트리 모두에서 뚜렷한 성능의 향상을 확인할 수 없었다(Fig. 6). 잔차 분석에서도 경향성과 분산의 감소가 눈에 띄지 않았다.
3.3 오차 분석
경향성을 일부 벗어난 3차 함수 SVM 회귀모델과 결정계수가 높은 GPR 회귀모델에 대해 잔차가 높은 데이터를 중심으로 오차의 원인을 분석하였다.
3.3.1 SVM 회귀 모델
SVM 회귀 모델은 커널함수의 차수가 증가함에 따라 점점 잔차의 무작위성이 증가하는 모습을 확인할 수 있었다(Fig. 4). 그러나 다항 함수 커널 중 가장 차수가 높았던 3차 함수 SVM에서 오히려 MAPE가 2차함수에 비해 증가하는 현상이 확인되었다(Table 3). 이를 확인하기 위해 잔차가 400 µm 이상으로 발생한 데이터에 대해 분석을 진행하였다.
Cu 상판 (1 mm)/Al 하판 (1 mm) 배열이고, 용접 속도 10 m/min, 레이저 빔 직경 83 µm와 340 µm의 조건에서 용접 후 측정된 레이저 출력별 용입 깊이와 잔차를 각각 Fig. 8(a), (b)에 나타내었다. 또한 나머지 조건은 동일하고 용접 속도 5 m/min, 레이저 빔 직경 170 µm 조건에서의 용접 후 측정된 레이저 출력별 용입 깊이와 잔차는 Fig. 8(c)에 나타내었다. Fig. 8(a)와 같이 유사 용접조건에 대해 데이터의 개수가 충분할 때 잔차의 분포는 안정되게 나타났으나, Fig. 8(b), (c)와 같이 근접한 조건에서 데이터의 개수가 1개 또는 2개로 작고 유사한 용접조건 그룹과의 용입차이가 클 때 잔차가 크게 나타난다.
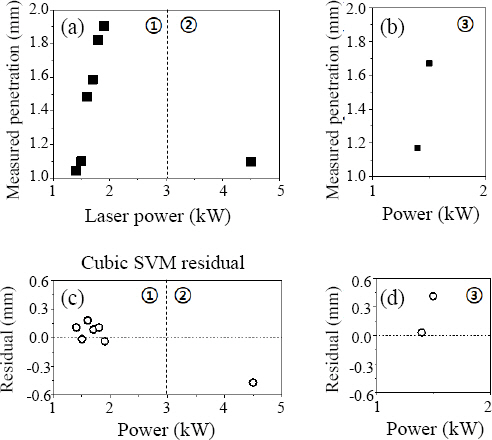
Penetration and residual plots for the cubic kernel SVM regression model. (Materials: Cu 1mm (top) and Al 1mm (bottom). Welding conditions: ① 83 µm laser beam diameter and 10 m/min welding speed; ② 340 µm laser beam diameter and 10 m/min welding speed; ③ 170 µm laser beam diameter and 5 m/min welding speed)
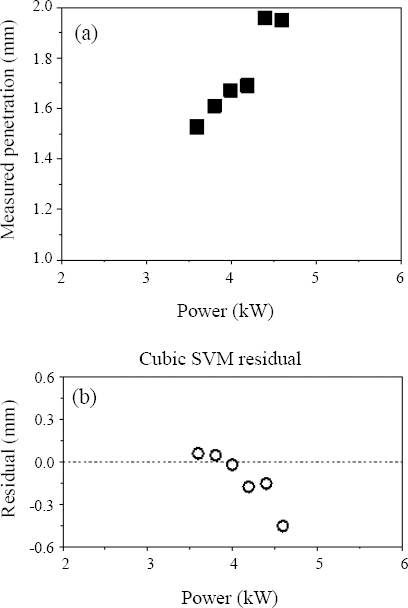
Al 상판(1 mm)/Cu 하판(1 mm)배열이고, 용접 속도 10 m/min, 레이저 빔 직경 340 µm의 조건에서 용접 후 측정된 레이저 출력별 용입 깊이와 잔차를 Fig. 9에 나타내었다. 레이저 출력이 증가하며 용입 깊이도 같이 증가하는 추세를 확인할 수 있었다. 하지만 용입 깊이 2000 µm일 때 완전 용입이 일어나 더이상 용입 깊이가 증가하지 않았고, 이에 따라 최대 출력인 레이저 출력 4590 W에서의 잔차가 크게 나타났다.
3.3.2 GPR 회귀 모델
회귀 모델 중 가장 높은 성능을 나타냈던 지수 GPR회귀모델에 대해서 잔차가 높은 데이터를 정밀 분석하였다. Al 상판(0.5 mm)/Cu 하판(0.3 mm) 배열이고, 레이저 빔 직경 83 µm, 용접 속도 30 m/min 조건에서 용접 후 측정된 레이저 출력별 용입 깊이와 잔차를 Fig. 10에 나타내었다. 잔차는 레이저 출력 1300 W의 조건에서 40 µm 정도의 특징적인 값을 보였고, 용입깊이 측정값을 확인한 결과 동일 조건에서 측정된 서로 다른 각각의 데이터간 실제 측정값의 차이가 75 µm로 큰 차이를 보여, 이와 같은 측정오차가 잔차의 원인이다.
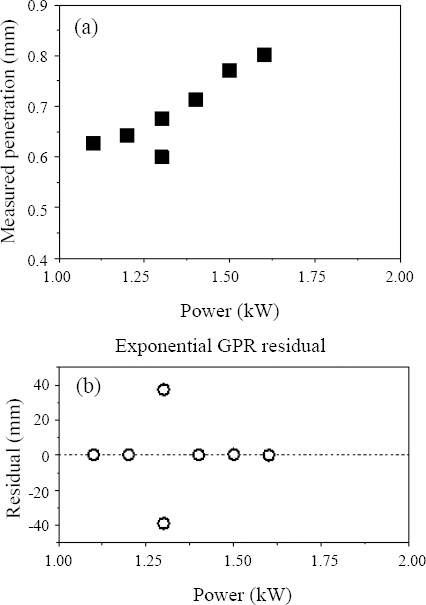
Penetration and residual plots for the exponential kernel GPR regression model (Materials: Al 0.5 mm (top) and Cu 0.3 mm (bottom). Welding conditions: 83 µm laser beam diameter and 30 m/min welding speed)
Cu 상판(0.3 mm)/Al 하판(0.5 mm) 배열이고, 레이저 빔 직경 20 µm와 83 µm, 용접 속도 30 m/min 조건에서 용접 후 측정된 레이저 출력별 용입 깊이와 회귀모델의 잔차를 Fig. 11에 나타내었다. Fig. 11의 오른쪽에 삼각형으로 표시된 지름 83 µm의 레이저로 용접한 용입 깊이는 레이저 출력이 증가할수록 증가하는 경향성 있는 모습을 확인할 수 있다. 그리고 잔차도 비교적 0 근처에서 일정함을 확인할 수 있다. 하지만 Fig. 11의 왼쪽에 사각형으로 표시된 레이저 빔 직경이 20 µm 일 때 800 W-900 W 구간에서 측정된 용입 깊이의 값에서 급격한 상승이 있었음을 확인했고, 이러한 용입 깊이의 측정 오차가 잔차에 영향을 주었음을 확인할 수 있다.
4. 결 론
본 논문은 Al/Cu 박판 이종재료 겹치기 레이저용접부의 제시된 변수(배열, 상판 두께, 하판 두께, 용접 속도, 레이저 출력 및 빔직경)에 대한 용입 예측에 기계학습을 적용하여 가장 우수한 지수 GPR 모델에서는 최소 오차율 0.2%, 결정계수 1의 회귀 모델을 얻었으며, 자세한 결과는 아래와 같다.
1) 선형회귀 모델, 의사결정 트리, SVM 회귀 모델, 회귀 트리 앙상블, GPR 회귀 모델에 기반한 총 19개의 기계학습 회귀 모델을 이종재료 레이저용접부의 다변수 용입예측에 적용하고 모델의 성능을 평가하였다.
2) 각 분류별 가장 성능이 좋은 모델의 절대 평균 오차율과 결정계수는 각각 상호작용 선형회귀모델 8.48%, 0.9, 조밀 의사결정트리모델 7.85%, 0.94, 조밀 가우시안 SVM 5.57%, 0.98, 부스팅 트리 9.63%, 0.92, 지수 GPR 0.2%, 1.0이다.
3) 차수가 낮은 회귀 모델인 선형회귀 모델, 의사결정 트리, 회귀트리 앙상블의 경우 잔차의 경향성이 나타나며 비교적 절대 평균 오차율과 결정계수가 낮았다.
4) 차수가 무한대로 확장 가능한 가우시안 커널을 사용한 SVM회귀 모델과 GPR에서 비교적 좋은 성능을 보였고, 이를 통해 이종재료 레이저용접부의 용입 예측에 충분히 높은 차수가 필요한 것을 확인하였다.
5) 3차 SVM 회귀 모델과 GPR의 진단결과 잔차의 분포를 벗어난 특징적인 오차는 각각 데이터의 부족과 측정 오차문제에서 야기됨을 확인하였다.
따라서, Al/Cu 박판 이종재료레이저 용접부의 용입깊이는 충분히 높은 차수의 기계학습 예측모델을 이용할 경우 정밀한 모델링이 가능함을 확인하였다,
Acknowledgement
This research was supported by the MOTIE (Ministry of Trade, Industry, and Energy) in Korea, under the Fostering Global Talents for Innovative Growth Program (P0008750) supervised by the Korea Institute for Advancement of Technology (KIAT)