1. Introduction
Nowadays, welding is used widely for connecting the members made of metal. Welding as other joining techniques has its own consequences and disadvantages. Residual stresses and distortions can occur near the weld bead due to localized heating during the welding process and subsequent rapid cooling. High residual stresses in regions near the weld may promote brittle fractures, fatigue, or stress corrosion cracking. Meanwhile, residual stresses in the base plate may reduce the buckling strength of the structure members and overall load bearing capacity. Therefore, the welding residual stresses must be minimized to control them according to the respective requirements1).
Previous investigators have developed several methods, including heat treatment, hammering, preheating, vibration stress relieving, and weld sequencing to reduce the residual stresses attributed to welding. However, choosing a different welding sequence is a simpler and more efficient method for reduction of welding residual stresses. This is also due to the fact that post-weld treatments cannot be applied to all welded structures. Therefore, developing an available welding sequence and accurately predicting welding residual stresses for welded joints are necessary for achieving the safest design.
Research on finding optimum welding sequences dates back to the 1940s2) and 1950s3) and considerable progress has been done in this field ever since. Not only is the distortion dependent on the welding sequence but also the residual stresses4). Here, the stresses have been calculated elastically and superposed for all welding passes on multi-pass butt-welded pipe joints. The superposed result is in fair agreement for the real distribution of the residual stresses and has been applied to find a welding sequence to minimise the distortion. It is also possible to perform numerical analysis in order to find an optimum welding sequence5). Welding simulation has been performed on a circular weld where only the radial distortion is of concern. The welding sequence has been optimised using a genetic algorithm and is a more or less arbitrary combination of eight subwelds. Using this optimal sequence, welding distortion is reduced by 80 %. For continuous welding; i.e., welding in one run without stopping, the radial displacement is significantly higher compared to the optimum welding sequence. However, there is still homogeneous radial shrinkage which cannot be avoided. Unfortunately, no explanation is given concerning why the optimum sequence yields better results. The influence of welding sequence for GMA welding of butt-welds and the effects on residual stresses has been investigated by Teng at al.6). Symmetric welding caused the lowest residual stresses while backstep and progressive welding show the same results. However, the stresses oscillate in the direction of the weld seam due the welding sequence. Zhang7) reported numerical simulations of GMA welded T-Joints. It has been concluded that the welding sequence can reduce the amount of bending distortion by approximately 25 %. However, neither the material model is explained, nor is it clear how the welding sequences are employed. Schwenk8) reported a reduction of 37 % of the welding distortion of an electron beam welded (circular) gear wheel using multiple beams in parallel. Lin9) employed different welding sequences for the packaging of butterfly laser diodes. The welding distortion was reduced by a factor of five using the optimum sequence.
Optimized welding sequences are not only applied in order to minimise distortion and residual stress, but also to minimise the total time required to weld a com- ponent. Neural network algorithms, which like genetic algorithms are also a stochastic optimisation method, have been presented in several references10-12) for minimizations of the welding time by optimisation of robot movement. A genetic algorithm13) has been presented in order to find a distortion and cycle time minimising welding and clamping sequence for resistance spot welding of an automotive vehicle body assembly.
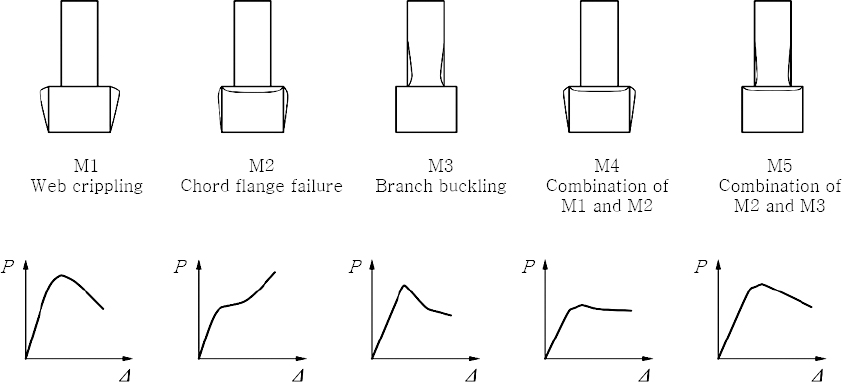
A T-joint has been chosen in the current study due to its prevalence in hollow steel structures as well as its relatively simple failure mode, which allows for an easier validation of the results obtained. In the majority of T-joint hollow sections, the brace member is under compression. The resistance of the joint mostly relies on the compression stability of the chord side walls, for the brace under compression. Fig. 1 shows the common failure modes for a compressively loaded T-joint.
In the present research work, four case studies have been chosen to provide experimental data for the model validation and comparisons. The case studies all include a T-joint made by square hollow sections as shown in Fig. 2 with the coordinate system adopted. are the brace height, width and wall thickness. are the height, width and wall thickness of the chord.
Fig.┬Ā2
Definition of the joint geometry and coordinate system used for all spatial results in the present study
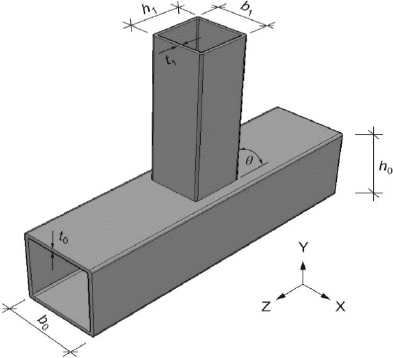
The branch or the brace has been chosen to be smaller than the chord member as in most of cases in practice. The brace has a height of 600 mm, width of 100 mm and thickness of 4 mm. The chord is 1200 mm long, width of 200 mm and wall thickness of 6.3 mm. The members are welded using MAG (Metal Active Gas). The brace is located vertically on the face center of the chord forming an unequal T-joint. Both members are made from the same material S355.
Fig. 3 and Fig. 4 present the case studies analyzed in this publication. Four different cases are studied experimentally. However, more cases are involved in the numerical investigations in order to deliver a better conclusion. All joints are welded with the same machine, same parameters at the same institute (FMPA Cottbus). Welding has been done manually. According to the size of the welds and members, it is difficult to perform welding with automatic welding machines, so called robots. A great effort has been made in order to keep the weld throat thickness more or less the same along the weld (a = 5 mm). From the first case, three joints are prepared for statistical analysis, hence they have been welded and undergone loading sooner. Arrows in Fig. 3 present the welding direction and the circle filled elements present the start and end points of welding.
2. Finite element modelling
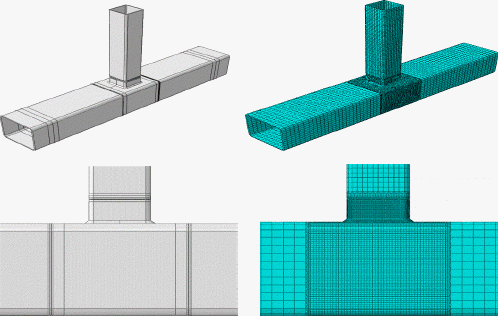
Finite element modelling is employed to simulate what is happening in reality. To obtain results which are close to those obtained from the experimental tests, FEM requires sufficient data such as the geometry itself, boundary conditions, loading and material properties. Sufficient data increases the accuracy of the results obtained and requires high attention and in some cases parametric studies. In the present work the FE software ABAQUS14) is used. The same model is built for all the cases listed in Table 1 as the only variable is the weld and its respective sequences. The geometry of the model with required partitions for mesh generation is shown in Fig. 5. The finite element solution is highly dependent on the mesh density. Meshing has also a great influence on computation time. The basic problem in welding is the discretisation of a domain holding a localised region with large gradients in field variables. Thermal, microstructural and mechanical effects require the weld zone to be discretized in millimeter sized elements while the far field region can be coarsely meshed. The mesh has been generated using ABAQUS and by element set definition, parts have been introduced in an input file to be used in SYSWELD15).
Table┬Ā1
Cases considered in the numerical (N) and experimental (V) investigations
2.1 Material properties
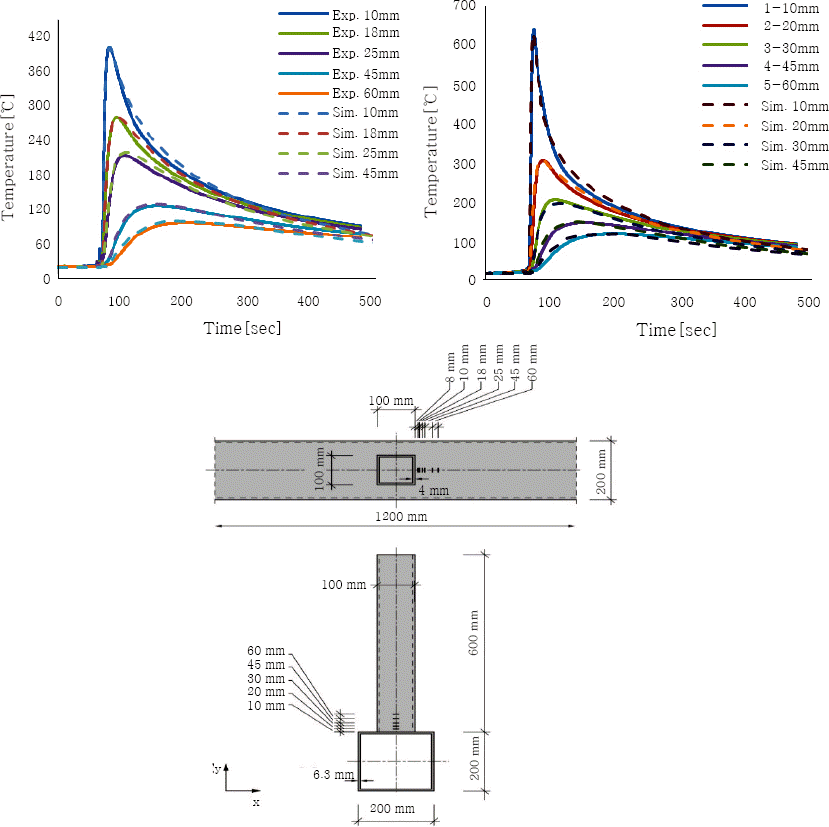
S355 steel has been chosen for both the chord and the brace. The material model takes into account elastoplastic laws. Phase transformation is not taken into consideration. ABAQUS model has been covered with the material properties as in SYSWELD. However, the mechanical properties of the material at room temperature are obtained experimentally from testing 8 specimens by means of coupon test. Some of the thermal and mechanical properties can be seen in the following diagrams, Fig. 6. As for the mechanical properties, the PoissonŌĆÖs ratio is 0.3 and the evolution of the YoungŌĆÖs Modulus and yield stress with respect to temperature can be seen in Fig. 7. The hardening model used is the isotropic one.
2.2 Welding simulation
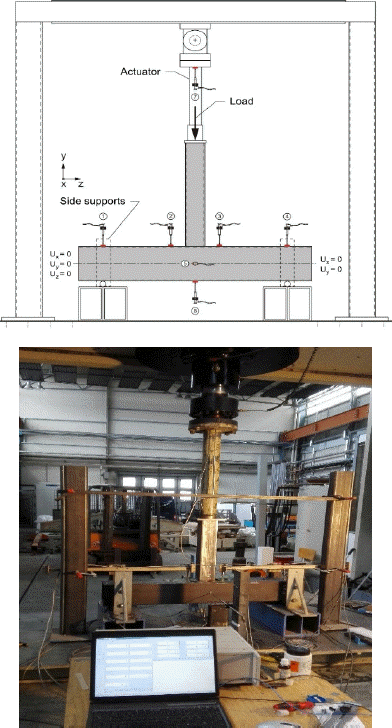
A FE based welding simulation was performed in Abaqus AWI. The Abaqus Welding Interface (AWI), introduced in this paper, exists in the form of an Abaqus/CAE Plug-In capable of building a welding finite element model. At first, the CAD geometry has been imported into AWI. In the next step, beads, passes and chunks have been defined. AWI automatically considers the material properties, geometry and mesh defined in Abaqus, for generating the thermal and structural models. Parameters such as the Stefan-Boltzmann constant, target torch heat up temperature, weld material initial melt temperature and sink temperature were kept as default values. The cooling rate is significantly influenced by the film coefficient value, so a small value (2.5e-05 W/mm2 C) was used. The numerical model was developed in Abaqus 6.11-3 using solid elements. The model was later transferred to Abaqus 6.14-2, as some functions regarding the simulation of the weld could only be performed there. As it can be seen, the mesh is more refined near the weld seam and coarser in the remaining parts, in order to reduce the analysis time and to avoid numerical convergence problems. Heat transfer elements DC3D8, DC3D6 and DC3D4 were used for the thermal analysis and stress elements C3D8, C3D6 and C3D4 were used for mechanical analysis. A parallel welding simulation has been performed for each single case. The same geometry and mesh has been used in SYSWELD. Fig. 8 presents the mechanical boundary conditions for both the welding and loading process adopted for numerical and experimental investigations. (a), (b), (c) have been adopted in loading and (d) presents the boundary conditions adopted for welding simulation. The heat source model used is the GoldakŌĆÖs double ellipsoid. Convective and radiative heat transfer has been assumed. The total energy was fitted along the 1D elements of the welding trajectory. The welding parameters used can be seen in Fig. 9 along with an image taken from the numerical simulation showing the laser spot temperature distribution. Red sections in (a) and (b) present the areas at which the boundary conditions have been applied. Red arrow in (c) indicates the direction of the load which has been applied on the upper surface of the vertical member. The red circles in (d) try to clarify the 4 nodes that have been used to restrain the joint when welding.
In order to validate the numerical model, the simulation temperature/time curves have been compared to those measured during the experiment at different distances shown in Fig. 10. The simulation results for the temperature show a very good agreement with those from the experiment.
3. Experimental tests
The experiments were carried out at the FMPA Cottbus. The SHS joints were manually welded by means of a MAG process. Temperature probes have been placed at specific locations in the vicinity of the weld bead. The experimental welding process can be seen in Fig. 11. The welding parameters, Current 230 A and Voltage of 22 V have been used for welding of all specimens. Welding boundary condition have been applied as shown in Fig. 8 (d).
After allowing the welded joints to cool down to room temperature, the samples were subjected to a compressive test, as seen in Fig. 5. The joints were all loaded under the same loading condition under brace concentric loading using a 2000 kN testing machine. The load was applied using stroke control at a rate of 3 mm/min up to failure. The (L/h) ratio of the chord was carefully selected as per recommendations for nodal supports in the literature. Testing the specimens requires prediction of failure modes which was done according to EN 1993-1-8.
4. Results
The numerical (ABAQUS and SYSWELD) and experimental results of load bearing capacity of the joints are plotted in Table 2 and Fig. 13. Reverse skip welding reflects a difference close to zero for the influence of direction, hence it is neglected and replaced by a widely adopted welding sequence scheme back-step welding.
Table┬Ā2
Maximum load reached for the investigated numerical and experimental cases
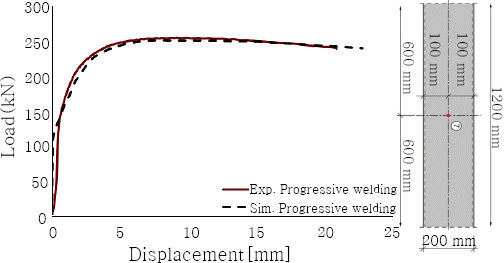
Fig. 14 shows the load vs displacement from both software used. Both curves offer the same elastic behavior. However, ABAQUS tends to yield earlier. Compared to the experimental results shown in Fig. 13, ABAQUS offers quite the same yielding behavior as SYSWELD. Obviously, the early yielding in ABAQUS influences the plasticity and hence the maximum load reached differs slightly compared to SYSWELD. The maximum load reached in SYSWELD is 260 kN and in ABAQUS 258 kN. As both software offer more or less the same behaviour for further evaluation (load-displacement) the results from SYSWELD are only compared with the experimental outcomes.
Apart from the brace member which is directly influenced by the concentrated force applied and shows the biggest deformation, the comparison of other points have been also done which helps a better validation of results. Fig. 15 illustrates the load vs deflection behavior of the points 3 and 4. Both points are located at 60 mm away from the weld beads on both sides. As it can be seen the curves follow the same trend with very minor differences. Due to a high magnitude of load applied the chord face faces a high compressive load which leads to chord face failure. Close results of both sides also point out the zero or very small tolerance in the brace member while loading. Due to the nature of the closed section tested in this work and the kind of boundary conditions adopted, points 1 and 2 experience a maximum vertical displacement magnitude of -1.5 mm on both sides.
After the chord face experiences a high compressive load and moves towards inside, the chord side walls start crippling out. The magnitude of this crippling is shown in Fig. 16 for points 5 and 6 which are located in the mid-surface on both sides of the chord member. A symmetrical deformation was expected as the centric loading allows for prediction. Fig. 17 shows the load- displacement behavior at point 7 which is located at the bottom surface and in the middle of the chord member. A maximum deformation of -23 mm has been measured after the loading process. The results show a good trend until the end of the loading process.
After an observation of reduction in gain of strength in the joints for better underpadding of the influence of various welding sequences on the load bearing capacity two further cases have been performed numerically. Back step welding, as skip welding (4 weld), involves 4 start and end points in the simulation of welding. However, the last numerical case adopted in this work involves 8 start and end points. Fig. 18 shows the load vs deflection for all numerically investigated cases. As it can be seen the first case (progressive welding) bears a higher load compare to other cases with 260 kN. The gain in strength drops by increasing the number of welds and reaches its minimum value in the last case (skip welding with 8 welds) with a magnitude of 237 kN. Compared to the first case, gain in strength drops by -20 %.
For a better observation and also to compare the stress results, points on the midline of top surface of the chord member have been picked as shown in Fig. 19. The aim behind selecting these nodes has been plotting the stress transition from the weld bead to the heat affected zone and then to unaffected areas (only surface nodes were considered). The stresses are studied in two different phases. First phase goes through stress distribution after the joint cools down for a time period of 550 seconds and the second phase offers the residual stresses distribution induced by loading.
Fig. 20 shows the longitudinal stress distribution with respect to the line selected along which the stress results were exported. As it can be seen both software are in a good agreement with some minor magnitude differences. The first case presents the highest tensile stresses at the weld bead as well as the second case. However, a drop of 170 MPa is observed at the weld toe for the third case as the line meets start and end points at the weld toe. Reduction in tensile stresses for the third case has influenced the compressive stresses which shaped by getting away from the weld. Higher compressive stresses for the third case with a magnitude difference of 80 MPa are observed in both software. It should be mentioned the difference between the stress distributions of all cases is only visible before the load application process. After the loading process all joints behave the same in terms of magnitude and the pattern.
Fig.┬Ā20
Stress distribution SYSWELD (left) and ABAQUS (right) in x direction before the loading process

The transverse stress distribution for N1, N2 and N3 is illustrated in Fig. 21. For these stresses the same differences are kept. However, the discrepancies between ABAQUS and SYSWELD are more visible in transverse stresses than in longitudinal stresses. All the curves obtained from the cases follow the same trends with some magnitude relevant disagreements. As for longitudinal stresses, the highest tensile stresses are observed for the progressive welding (N1) and by increasing the number of welds these stresses face reduction. The reduction of tensile stresses is more visible in the weld toes than other areas with a magnitude of 45 MPa.
Fig.┬Ā21
Stress distribution SYSWELD (left) and ABAQUS (right) in z direction before the loading process.

For a better evaluation of results and differences, the Mean stresses are plotted for all the numerical cases in Fig. 22. As previously explained the stress distribution varies for different investigated cases. For progressive welding where only a continuous weld is involved the stress is distributed along the weld. N2 (b), clearly shows how two continuous welds could influence the stress distribution. As for the first case, stresses close to zero are observed close to the start and end points. Third case and fourth case behave nearly the same. The results of load bearing capacity also pointed out that these two welding sequence leave the same stress distribution. (c) and (d) are respectively skip welding and back-step welding. In both cases 4 welds are involved. The last numerically investigated case has been (e) skip welding with 8 welds involved. Compare to other cases stresses more tend to expand in the surrounding areas. Bigger number of welds means welds with shorter length and the same heat input applied which has led to higher tensile stresses at and around the weld toes. In all the cases compressive stresses are pretty the same distributed on the side wall edges of the chord member and the differences are only observed in the intersection area. For welding directions, start and end points please see Fig. 3 and Fig. 4.
5. Failure mode
All the joints have experienced the two most common failure modes under axial loading which are chord face and side wall failure. As it can be seen in Fig. 23 the vertical member (brace) on which the compressive load was applied, first started moving down. High compressive load applied on the brace forces the chord face to deform and this deformation on the chord face caused the symmetrical outward crippling of the chord side walls.
6. Conclusion
After the thermo-mechanical welding simulation was successfully simulated for the steel SHS joints, the compression loading test was performed. The results in terms of stresses were compared and many similarities have been found between the solutions offered by the two commercial software used. Measured results of longitudinal and transverse stresses have shown that various weld sequence schemes can lower the magnitude of residual stresses especially around the weld toe and in the heat affected zoon. The results were only obtained for a number of nodes on a selected line. However, a better evaluation of results in terms of stress distribution for the whole joint is necessary. The comparison of both software reflects minor differences. These difference reach their highest level in transverse stresses. This could only be explained by the difference in temperature iso-surfaces and lack of a proper heat source model in ABAQUS AWI. Gain in strength drops by increasing the number of start and end points, reaching a maximum value of -10 % when 8 start and end points are involved. The outcomes point out an important relationship. As the only variable in all cases investigated has been the welding sequences, so it could be clearly explained how stress concentration or so called the number of start and end points could highly influence the overall behaviour of the joints. Further experimental and numerical investigations are needed especially with focus on the areas between start and end points where the stress concentration tends to shape.


















 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print