전극 변위 신호를 이용한 저항 점용접 압흔 깊이 예측
Prediction of Indentation Depth of Resistance Spot Welding Using Electrode Displacement Signal
Article information
Abstract
Resistance spot welding is a crucial assembly process for vehicle body manufacturing. The quality of the weld joint significantly influences the rigidity and durability of the vehicle; therefore, it is necessary to inspect the weld quality. The indentation depth of the resistance spot welding joint is widely used as an indicator to evaluate the quality of welds. However, because indentation tests on resistance spot welds are typically performed by field workers, additional time and process are required for the tests. Moreover, several attempts to apply automatic methods have shown limitations in high efficiency and prediction accuracy. To address this problem, we measured electrode displacement using a linear variable differential transformer during resistance spot welding in this study. In addition, we established an estimated regression model using the measured electrode displacement data to predict the indentation depth. Multiple regression models were estimated through stepwise regression analysis, and the significance of the model was analyzed through analysis of variance and residual analysis. Indentation depth prediction was performed after the resistance spot welding process using the proposed regression model, and prediction accuracy higher than 93% was achieved. The coefficient of determination obtained for this model was 94.72%.
1. 서 론
저항 점용접(resistance spot welding)은 자동차 부품 조립의 주된 접합 공정이며, 다른 용접 공정들에 비해 높은 생산성을 가진다는 장점이 있다. 차체에 적용된 저항 점용접부는 자동차의 강성과 충돌 안전성과 밀접한 연관을 가지고 있기 때문에, 용접부의 품질 향상과 품질 유지는 중요하다. 그러므로 현장에서는 저항 점용접 공정 후에 용접부의 강도, 너깃 지름, 압흔 깊이(indentation depth)와 같은 품질 검사가 이루어지고 있다. 압흔 깊이(indentation depth)는 점용접부 품질을 평가하는 하나의 지표이며, 용접된 부품의 외관 품질과 용접부의 강성과도 높은 상관성을 가진다. 압흔 깊이에 대한 품질 평가는 일반적으로 작업자에 의해 직접 측정되기 때문에 별도의 공정이 필요하고 이로 인해 생산성이 저하되는 문제가 발생한다. 그러므로 이러한 문제를 해결하기 위해 기술 개발이 요구된다. 현재의 품질 검사 방법은 일반적으로 파괴 검사와 비파괴 검사를 통해 이루어지고 있다. 비파괴 검사의 경우, 일반적으로 용접 공정 중 측정되는 용접 신호인 용접 전류, 전압, 동저항, 입열량, 전극 변위 등의 신호를 기반으로 하여 품질을 예측하는 방식으로 이루어진다. 하지만 용접 생산 현장에 이러한 비파괴 검사 기술을 적용하는 것은 아직까지 제한적이며, 이러한 제약을 극복하기 위한 기술 개발이 필요한 상황이다.
압흔 깊이를 통한 용접 품질 평가 기술 개발을 위해 저항 점용접의 전극 변위를 활용한 실시간 품질 예측 및 검사 기술에 대한 연구가 활발히 수행되고 있다. Shin1) 등은 저항 점용접을 수행할 때 검출되는 2차 회로 공정 변수를 이용하여 용접부의 동저항을 모니터링하고, 이 동저항 패턴에서 용접 품질 판단에 필요한 인자들을 추출하여 용접 강도를 예측할 수 있는 회귀모델을 개발하였다. Podržaj2) 등은 전극 모양과 유사한 조명을 사용하여 전극 표면 전체에 걸쳐 거의 동일한 강도로 전극 표면을 비추었다. 그 결과 머신 비전을 사용하여 전극 변위를 측정할 수 있었다. Kusˇcer3) 등은 필드 프로그래머블 게이트 어레이(field programmable gate array, FPGA) 기술을 기반으로 한 임베디드 이미지 프로세서가 포함되어 있는 카메라를 사용하여 빠른 이미지 처리를 가능하게 하였고, 이를 기반으로 전극 변위의 실시간 모니터링이 가능한 기술을 개발하였다. Simonˇciˇc4) 등은 전극 팁의 변위를 이미지 처리 방식으로 측정하였고, 이는 기존 시스템의 단점인 시간 문제를 해결하였다. Kim5) 등은 서보건의 엔코더 데이터를 활용하여 전극 변위 값을 수집, 용접 품질 판단 기준으로 활용하기 위한 연구를 진행하였고, 부가적인 장치의 추가 없이 용접 품질 판단에 사용될 수 있는 시스템을 개발하였다. Zhang6) 등은 서보건의 엔코더를 사용하여 전극 변위를 측정한 후, 압흔 깊이를 실시간으로 모니터링하였다. Zhang7) 등은 전극 변위를 측정하기 위해 DA-5 직류 변압기 변위 변환기를 사용하였고, 전극 변위 곡선에서 추출한 매개 변수를 사용하여 다중회귀모델을 추정 후 전단인장강도를 예측하였다. 하지만 선형 가변 변위 변환기(linear variable differential transformer, LVDT)를 사용한 전극 변위 신호와 용접 품질 및 강도의 상관 관계에 대한 연구가 제한적이고 그에 대한 연구가 필요한 상황이다.
본 연구에서는 압흔 깊이에 대한 품질을 예측하기 위해 LVDT 전극 변위 신호를 기반으로 한 용접 품질 모델을 추정하였다. 전극 변위 신호 파라미터 정보를 사용하여 회귀 분석을 진행하였고, 후진제거법을 통한 다중회귀모형을 사용하여 모델을 추정하였다. 결정 계수는 94.72%의 예측 모델을 개발하였다.
2. 실험 절차
2.1 사용 재료 및 실험 조건
본 연구에서는 590, 780, 980 MPa급의 냉간압연강판을 사용하였으며, Table 1에 소재의 화학적, 기계적 조성을 나타내었다. 실험 조건은 저항 점용접의 주요 공정 변수인 용접 전류와 용접 시간의 변경에 따라 실험을 진행하였고, Table 2에 실험 조건을 나타내었다.
2.2 실험 장비
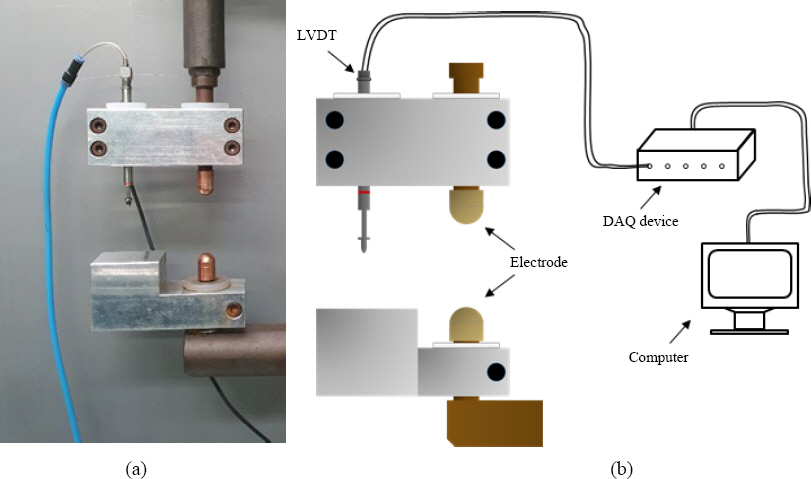
Fig. 1은 서보건과 LVDT 설치 장비와 전극 변위 측정을 위한 측정시스템의 모식도를 보여준다. 전극 변위는 LVDT를 사용하여 Fig. 1(a)에서와 같이 전극 양단에 지그(jig)를 고정시켜 전극이 용접부와 맞닿아 있는 순간부터 가압이 종료되는 시점까지를 측정하였다. 본 연구에서 사용된 LVDT는 공압 방식으로 최대 10 mm까지의 변위 측정이 가능하고, 센서의 높이에 따라 2 ㎛에서 35 ㎛ 오차(accuracy error)를 갖는 사양의 MARPOSS사의 FP50L 제품을 사용하였다. 전극 변위 신호(이하 LVDT 변위 신호)는 ADC(analog-to- digital converter)를 사용하여 50000 sample/s로 측정되었다. 또한, 실제 압흔 깊이(이하 실제 압흔 깊이) 측정을 위해 포인트 마이크로미터(point micrometer)를 사용하여 용접 후 압흔 깊이 측정을 진행하였다. 포인트 마이크로미터는 분해능 1 ㎛ 사양의 MITUTOYO사의 제품을 사용하였다.
2.3 다중회귀모델
회귀 분석은 반응변수와 하나 이상의 설명변수 간의 관계를 설명하는 통계적 방법이다. 그중에서 단순회귀모형(simple regression model)은 설명변수 하나만으로 반응변수 Y의 변화를 설명하기 위한 회귀모형이다. 하지만 설명변수 하나만으로 반응변수를 설명하기에는 설명력이 부족하고, 유의한 설명변수간 영향력 비교가 요구된다. 이로 인하여 설명변수가 2개 이상인 회귀모형에 대한 회귀모형에 대한 분석이 필요하다. 그러므로 본 연구에서는 설명변수 2개 이상을 사용하는 다중회귀모형(multiple regression model)을 사용하여 모델을 추정하였다. 특별히 k개의 설명변수의 값x1 , x2 ,⋯, xk에서 관측되는 반응변수Y1 ,Y2 ,⋯, Yn에 대하여 일반적인 형식은 다음과 같다.
Yi = β0 +β1x1 +β2x2 + ⋯ + βkxk
위와 같은 선형 관계를 가정한 모형을 다중회귀모형이라 한다. 여기서β0 와 β1 , β2 ,⋯, βk는 추정해야 할 회귀계수들이며, β0는 상수항을 나타낸다. 회귀 방정식은 예측 변수의 값을 예측된 값인Y^로 결합된다. Y^는 예측 변수의 선형 조합을 나타낸다. 각 예측 변수xk에 회귀 가중치βk를 곱한 다음 이러한 곱을 예측된 최종 값에서 모든 예측 변수에 대해 합산한다. 회귀 상수(β0 = MY -β1Mx1 -β2Mx2 ⋯-βkMxk)는 기준MY의 산술 평균과 모든 예측 변수(MX1 ⋯MXP) 평균의 함수이다. 회귀 상수는 평균MY^가 관찰된 기준 값의 평균과 같도록 예측 값을 조정한다. 모든 예측 변수가 평균이 0이 되도록 척도화가 되면, 회귀 상수는 기준MY의 평균과 같다. 예측 값Y^는 예측 변수 집합을 기반으로 한 관측 된 기준 값 Y의 최소 제곱 추정치이다. 회귀 방정식은 다른 예측 변수의 기여도를 넘어서Y^에 대한 각X의 고유한 선형 기여도를 나타낸다9).
3. 결과 및 고찰
3.1 용접 실험
용접 실험은 Table 2와 같이 전극 가압력은 2.94 kN으로 고정시키고 용접 전류 조건은 4, 5, 6, 7 kA, 용접 시간 조건은 250, 333, 417 ms로 실험을 진행하였다. Table 3은 용접 전류와 용접 시간별 단면 사진을 나타내었다. Table 3을 보았을 때 용접 전류와 용접 시간이 증가함에 따라 압흔 깊이와 용접부의 크기가 증가하는 특징을 가지는 것을 확인할 수 있다.
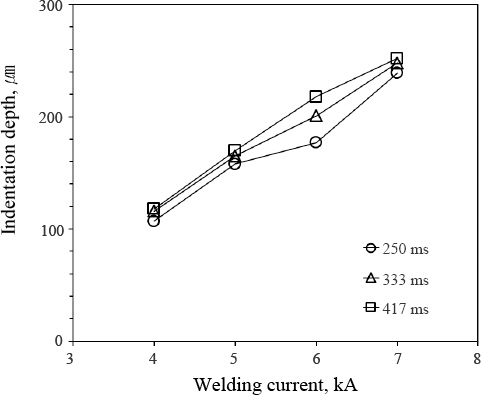
Fig. 2은 용접 전류에 따른 포인트 마이크로미터로 측정한 실제 압흔 깊이를 용접 시간별로 나타내었고, 각 조건에서 시험편 3개에 대한 평균값을 보여주고 있다. 실제 압흔 깊이는 용접 전류와 용접 시간이 증가함에 따라 증가하고 있다는 것을 알 수 있다.
3.2 압흔 깊이 측정
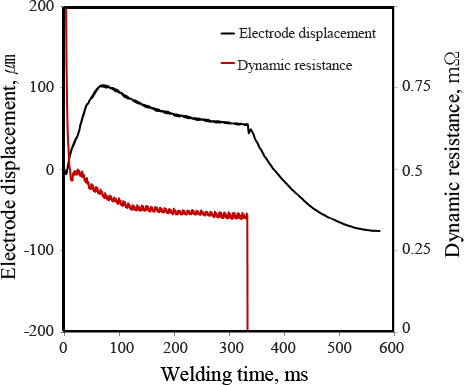
Fig. 3은 용접 전류 5 kA, 통전 시간 333 ms, 유지 시간 167 ms 조건에서 측정된 LVDT 전극 변위 신호 파형과 동저항 파형을 보여준다. LVDT 전극 변위 신호 파형과 동저항 파형은 전체적으로 유사한 곡선의 패턴을 가지지만, LVDT 전극 변위 신호 파형의 최대점이 동저항 파형의 베타 피크점(beta peak)대비 수십 ms의 지연되어 나타나는 특징을 가졌다.
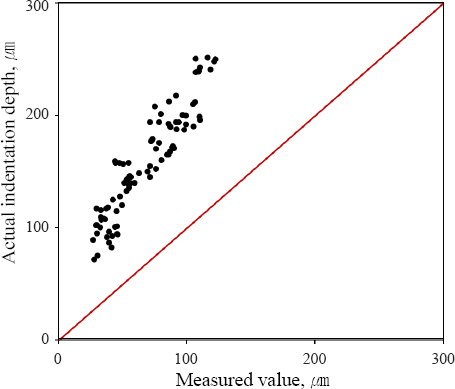
Fig. 4는 LVDT 전극 변위 신호를 통해 측정한 압흔 깊이와 실제 압흔 깊이의 비교 결과를 보여준다. LVDT 전극 변위 신호를 통해 측정한 압흔 깊이는 Fig. 3의 LVDT 전극 변위 신호 파형의 시작점 전극 변위에서 측정 종료점 전극 변위를 차를 통해 계산된 값이다. LVDT를 통해 측정된 압흔 깊이와 실제 압흔 깊이가 일치하지 않는 현상이 관찰되었으며, 이 차이의 주된 원인은 용접 후 냉각으로 인한 냉각 수축이라고 판단된다.
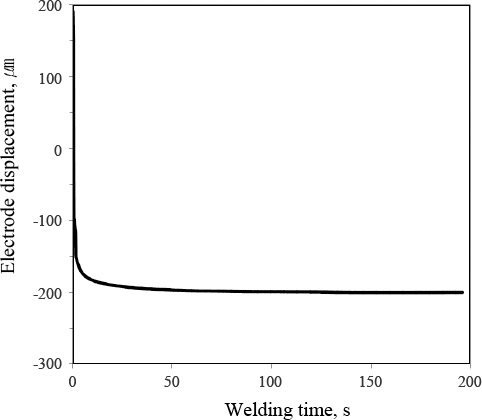
용접부의 냉각으로 인한 압흔 깊이 변화를 관찰하기 위해, 용접 종료 후 전극 가압을 약 200 s 정도를 유지했을 때의 전극 변위를 측정하였고 그 결과는 Fig. 5와 같다. 용접 종료 후에도 전극 변위는 감소하였고, 용접 종료 후 약 100 s까지 서서히 감소하였다. 그 후 특정 변위 값에서 수렴하였다. 이때 수렴하는 LVDT 전극 변위 값은 실제 압흔 깊이와 비교하였을 때, 일치하는 것을 확인하였다. 용접 종료 후 압흔 깊이는 유지 시간(hold time)을 길게 하여 충분히 냉각된 상태에서 LVDT 센서를 사용하여 측정하면 확인할 수 있지만, 고정된 공정 스케줄에 따라 진행되는 용접 공정에서는 이러한 방식의 압흔 측정은 불가능하다. 따라서 본 연구에서는 LVDT 전극 변위 파형을 통해 실제 압흔 깊이를 예측할 수 있는 모델을 개발하였다.
3.3 전극 변위 매개 변수
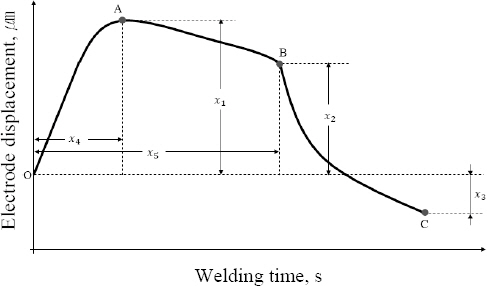
Fig. 6은 LVDT 전극 변위 신호 파형과 압흔 깊이 예측 모델 개발을 위해 선정한 특징점을 보여준다. 용접부의 열팽창, 냉각, 그리고 전극 가압력에 의한 전극 변위 특징을 표현하기 위해, 본 연구에서는 Fig. 6과 같이 3개의 특징점(A, B, C)을 선정하였다. 특징점 A는 LVDT 전극 변위 신호의 최대점이며, 특징점 B는 용접 전류의 통전이 종료되는 시점의 변위점, 그리고 특징점 C는 유지 시간의 종료 시점의 변위점이다. 전극 변위는 용접 초기 단계에 용접부 팽창으로 인해 특징점 A까지 급격하게 성장하여 최대 변위 값에 도달하였으며, 변위가 최대값에 도달한 이후 용융부의 면적이 넓어짐과 동시에 가압력에 의해 통전 종료 시점인 특징점 B까지 변위가 서서히 감소한다. 통전이 종료된 후에는 용접부의 냉각과 가압으로 인해 가압 종료 시점인 특징점 C까지 급격한 변위 감소가 나타났다. 선정된 3개의 특징점을 기반으로 한 압흔 깊이 예측 모델을 개발하기 위해, Fig. 6에 표현된 것과 같이 LVDT 전극 변위 신호에서 5개의 매개 변수(x1 , x2 , x3 , x4 , x5)를 선정하여 추출하였다. 특징점 A의 변위 값과 시간을 각각x1과x4로 표현하였고, 특징점 B의 변위 값과 시간을x2와x5로 표현하였다. 그리고 특징점 C의 변위 값을x3으로 나타내었고, 유지 시간은 167 ms로 고정하였기 때문에 특징점 C의 시간은 매개 변수에서 제외하였다.
3.4 압흔 깊이 예측 모델
3.4.1 매개 변수와 압흔 깊이의 상관 분석
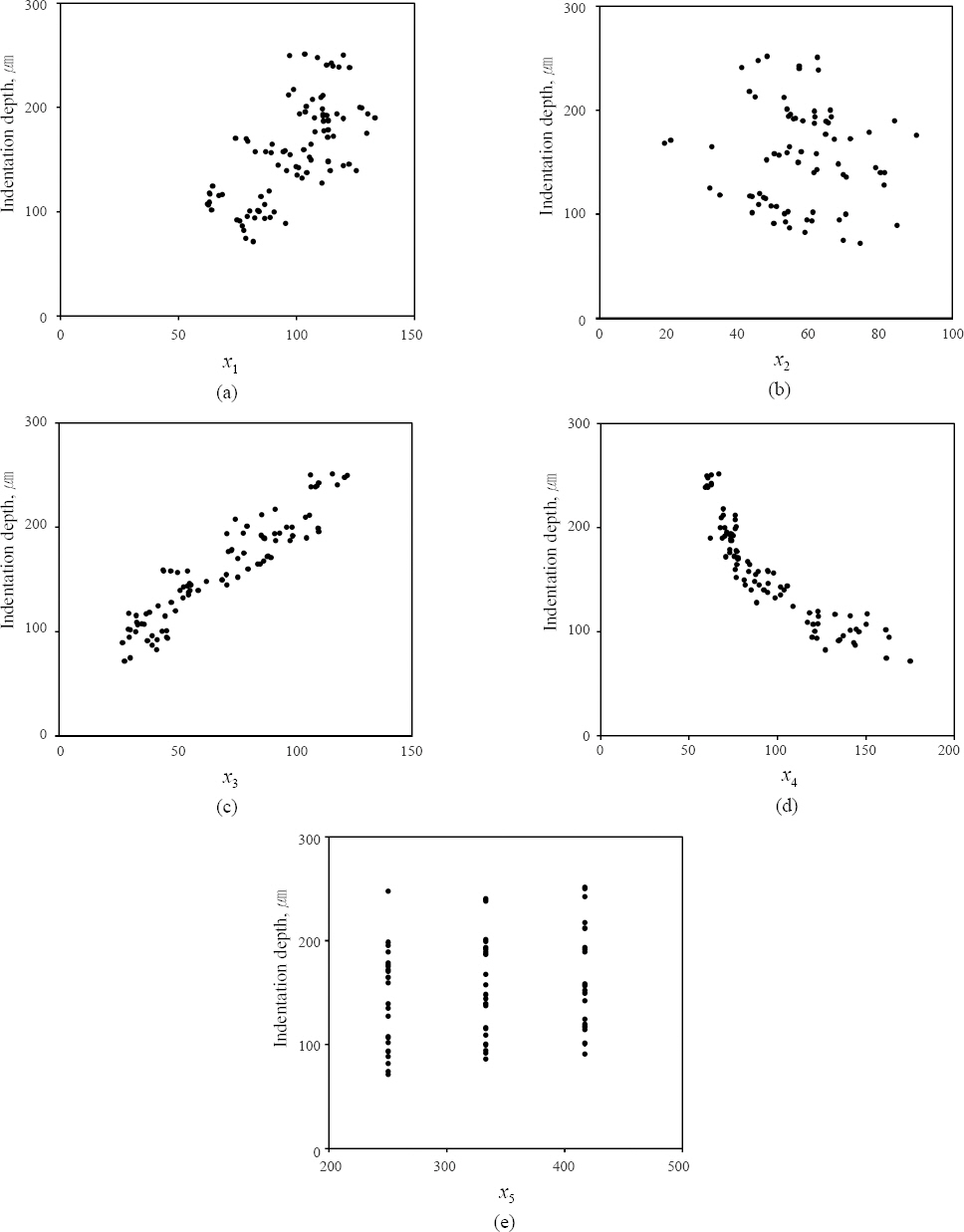
전극 변위 곡선에서 추출된 5개의 매개 변수가 독립 변수로서 종속 변수인 실제 압흔 깊이 간에 상관 관계에 대해 평가하기 위해 상관 분석을 진행하였다. 상관 분석은 두 변수 간의 선형 관계와 통계적 지표가 얼마나 밀접한지를 보여준다. 매개 변수와 실제 압흔 깊이의 상관 계수가 클수록 매개 변수가 압흔 깊이에 더 큰 영향을 준다. 5개의 매개 변수와 실제 압흔 깊이와의 상관 계수를 나타내는 분석 결과를 Table 4에 나타내었으며, 매개 변수 중에x2 , x3 , x4는 압흔 깊이와 높은 상관 관계를 가지는 것으로 확인되었다.
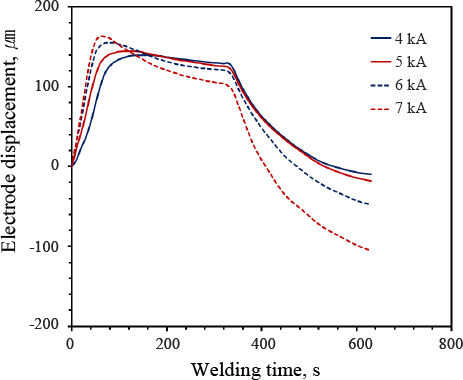
Fig. 7은 압흔 깊이 예측 모델용 5개의 매개 변수에 대한 실제 압흔 깊이의 산포도를 보여준다. Table 4의 결과와 같이, 매개 변수x3이 실제 압흔 깊이와 가장 높은 양의 상관 관계를 가지며, x4와x1역시 실제 압흔 깊이와 높은 상관 관계를 가진다. x4의 경우, 음의 상관 관계뿐만 아니라 비선형적 관계(거듭제곱, 지수) 역시 가지고 있다. X2와x5는 실제 압흔 깊이와 유의미한 상관 관계를 가지고 있지 않다. Fig. 8은 전류별 전극 변위 파형을 나타내는데, 용접 전류가 증가함에 따라x2 , x3는 증가하고, x4는 감소하는 것을 볼 수 있다. 압흔 깊이는 용접 전류가 증가함에 따라 증가하는 경향이 있으므로8), x2 , x3 , x4는 압흔 깊이와도 높은 상관 관계가 나타난 것으로 보인다. X5는 상관 계수가 0.109이며 압흔 깊이에 대해 효과가 분명하지 않다고 판단된다.
3.4.2 압흔 깊이 예측 모델 및 회귀 분석
본 연구에서는 다중회귀를 사용하여 용접 품질 예측 모델을 추정하였다. Fig. 6에서 보여주는 것과 같이x1 , x2 , x3 , x4 , x5을 모델의 독립 변수로 사용하였다. Table 4와 같이, 독립 변수는 종속 변수와 관련이 있을 뿐만 아니라 독립 변수 서로 간에도 관련이 있다. 이 상황에서는 모델의 독립 변수는 다른 입력 변수의 결과에 방해하는 역할을 할 수 있다. Table 4에서x2와x3사이의 상관 계수는 0.891, x2와x4사이의 상관 계수는 -0.884, 그리고x3와x4사이의 상관 계수는 -0.879이다. 이와 같은 계수가 큰 두 매개 변수를 동시에 독립 변수로 입력하면 여러 상호 작용 현상이 발생하고 모델의 예측 정확도가 떨어진다. 그러므로 본 연구에서는 단계적 회귀 방식인 후진 제거법을 사용하여 모델을 추정한다. 후진 제거법은 회귀식에 모든 변수를 입력한 다음 순차적으로 제거하는 변수 선택 방법이다. 후진 제거법은 종속 변수에 가장 적은 영향을 주는 변수부터 하나씩 제거하면서, 모든 변수가 유의하며 더 이상 제거할 변수가 없을 때까지 제거한다. 최대 차수가 2차인 회귀 모델을 추정하였으며, 유의 수준(α) 0.05를 기준으로 후진 제거법을 통해 유의하지 않은 항을 모델에서 제거하였다. 총 17단계의 후진 제거를 통해 압흔 깊이 예측을 위한 최종 모델을 추정하였으며, Table 5는 후진 제거의 1, 9, 17단계의 결과(모델의 계수, 각 항의 P value)를 보여준다. 1단계의 경우, 완전 2차 모델(full model)을 기술하고 있으며, 후진 제거의 단계가 거듭될수록 유의 수준 0.05를 기준으로 유의하지 않은 인자가 제거된다. 비록 최종 17단계의 축소 모델(reduced model)의 결정 계수가 완전 모델의 결정 계수(95.61%) 보다 약 1% 정도 낮은 값을 가지지만, 수정 결정 계수의 값은 94.42%로 완전 모델의 값보다 높은 값을 가지는 것으로 계산되었다.
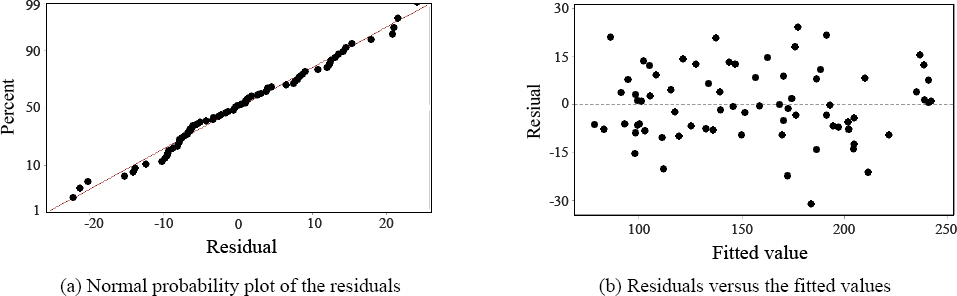
최종 모델은 Eq. (1)과 같으며, 잔차 분석 결과는 Fig. 9와 같다.
정규 확률도 검사 결과(Fig. 9(a)), 거의 대부분의 점들이 직선 주변에 가까이 분포하고 있으므로 오차는 정규분포를 따른다고 할 수 있다. 적합지-표준화 잔차 검사 결과(Fig. 9(b)), 잔차들이 전체적으로 0에 대하여 대칭적으로 분포하고, 설명변수의 값에 따른 잔차의 산포가 크게 다르지 않으며, 점들이 특정한 형태를 띠면서 나타나지 않았기 때문에 분석 모형으로 추정된 다중회귀모델을 적합하다고 판단된다.
3.5 압흔 깊이 예측 모델의 유효성 검사
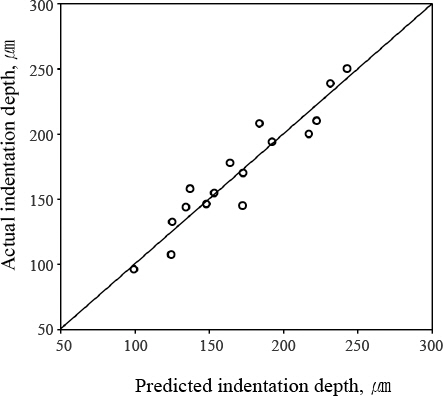
추정된 모델 Eq. (1)를 사용하여 압흔 깊이를 예측하였다. 예측을 위해 추가적으로 측정된 16개의 데이터가 사용되었으며, 실제 측정된 압흔 깊이와 예측된 압흔 깊이의 비교 결과를 Fig. 10에 나타내었다. 측정값과 예측값의 차이는 평균 11 ㎛, 예측 정확도는 평균 93.33%가 나타났다. KS B 0850 표준의 경우, 압흔 깊이를 판 두께의 10% 또는 0.15 mm 중 어느 쪽이든 큰 쪽의 값을 초과해서는 안 된다고 규정하고 있다. 따라서 본 연구에서 추정한 모델과 KS B 0850 표준을 기반으로 할 경우, 압흔 깊이에 의한 용접 품질을 판정할 수 있다고 사료된다.
4. 결 론
본 연구에서는 LVDT 센서를 사용하여 전극 변위를 측정할 수 있고, 전극 변위 파라미터 정보를 사용하여 예측 모델을 다중회귀모형을 이용하여 추정하였다. 본 연구의 결과를 요약하면 다음과 같다.
1) 압흔 깊이 예측 모델을 추정하기 위해 전극 변위 곡선에서 5개의 매개변수를 선정한 후, 이들 매개변수와 압흔 깊이 사이의 상관 관계를 분석하였고 주요한 매개변수를 선정하였다.
2) 다중회귀모형을 사용하여 후진 제거법을 통해 모델을 추정하였으며, 결정 계수(R2)는 94.72% 예측 모델을 개발하였다.
이 연구의 결과는 용접 품질 검사의 자동화 기술에 대한 지식 상태에 기여한다. 본 연구는 용접 품질 검사에 사용되는 LVDT를 기반으로 한 전극 변위 측정시스템을 이해하고, 저항 점용접의 압흔 깊이에 대한 품질을 자동으로 예측할 수 있기 때문에 자동차 산업에서 특히 사용될 것이다. 향후 작업은 추가적으로 다양한 소재, 두께, 도금에 대한 database 구축을 통해 모델을 개선할 것이고, deep neural network(DNN), convolu- tion neural network(CNN) 등 machine learning 이론을 적용하여 모델을 개선할 예정이다.
Acknowledgements
본 연구는 한국생산기술연구원 기관주요사업(kitech EH-21-0003) 및 산업통상자원부의 산업기술혁신사업(KM210027)의 지원으로 수행한 연구입니다.