Optimizing the Friction Stir Spot Welding Parameters to Attain Maximum Strength in Al/Mg Dissimilar Joints
Article information
Abstract
This paper discusses the optimization of friction stir spot welding (FSSW) process parameters for joining Aluminum alloy (AA6061-T6-jwj-34-3-23) with Magnesium alloy (AZ31B) sheets. Prior to optimization an empirical relationship was developed to predict the Tensile Shear Fracture Load (TSFL) incorporating the four most important FSSW parameters, i.e., tool rotational speed, plunge rate, dwell time and tool diameter ratio, using response surface methodology (RSM). The experiments were conducted based on four factor, five levels central composite rotatable design (CCD) matrix. The maximum TSFL obtained was 3.61kN, with the tool rotation of 1000 rpm, plunge rate of 16 mm/min, dwell time of 5 sec and tool diameter ratio of 2.5.
1. Introduction
Joining of dis-similar materials is required in many engineering applications for assembling of different configurations, thicknesses and also of dissimilar alloys. Recently, the automobile industry is actively considering a number of alternative welding technologies that would enable the increased use of lightweight and high-performance materials like aluminum and magnesium1). There are many problems that occur during the fusion welding of aluminum and its alloys such as hot- cracking, porosity, oxidation and alloy segregation2-4). Fusion welding of magnesium and its alloys also presents certain problems like complex thermal stress and severe distortion, porosity and crack in the weld zone, and excess eutectic formation5). Friction Stir Welding (FSW), a solid state welding process, patented by The Welding Institute (TWI), eliminates most of these problems6). In FSW, metallurgical bonding between similar or dissimilar materials can be created without melting as it is a solid-state welding process.
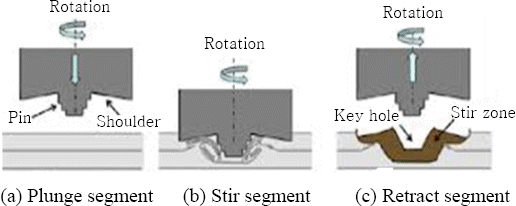
Friction stir spot welding (FSSW) is a variant of friction stir welding (FSW), in which a series of spot welds are used. The principle of the process is illustrated in Fig. 1. A non-consumable rotating tool, with a probe pin, plunges into the upper sheet and with a backing tool beneath the lower sheet to withstand the downward force (Fig. 1a). The tool rotational speed and tool shoulder are kept for an appropriate time to generate frictional heat between tool shoulder and work piece (Fig. 1b). Due to frictional heat, the softened material adjacent to the tool deforms plastically, and a solid state bond is produced between upper and lower sheets. Finally, the tool is withdrawn from the joint (Fig. 1c).
FSSW process parameters such as tool rotational speed, plunge rate, dwell time, and tool diameter ratio influence the mechanical and metallurgical properties of the joints. In order to attain superior mechanical properties, it is necessary to optimize the FSSW process parameters. One of the most efficient methods to optimize the FSSW process parameters is Response Surface Methodology (RSM). RSM is a collection of statistical and mathematical models, which is a very useful tool to analyze and model engineering problems7). In this method, the main objective is to optimize the response surface that is influenced by various FSW process parameters. The steps involved in this method are: (i) designing a series of experimental condition based on the factor and its level, (ii) deriving a mathematical model using second order equation with best fit, (iii) finding the optimum process parameters that produces a maximum response value, and (iv) indicating the direct and interaction effect of the process parameters through two or three dimensional plots8,9).
Babu et al10) investigated the effect of tempered conditions of base material (AA2014) on the joint strength and the optimized FSSW process. Karthikeyan et al11) optimized FSSW process parameters such as tool rotational speed, plunge rate, plunge depth and dwell time on AA2024 aluminum alloy using RSM, and found that the maximum TSFL was achieved at 9.39 kN under the welding conditions of tool rotational speed, plunge rate and plunge depth of 1000rpm, 13.56 mm/min, 5.178 mm, and 5.1 sec respectively. Ramanjaneyulu et al12) optimized the yield strength, tensile strength and ductility of friction stir welded AA2014-T6-jwj-34-3-23 aluminum alloy using RSM, and also found that AA 2014-T6-jwj-34-3-23 aluminum alloy welded with hexagonal tool pin profile had the highest tensile strength and elongation as compared to the conical, triangle, square, and pentagon pin profile, using a four factor five level central rotatable design matrix.
Many researchers worldwide have already applied RSM to optimize friction stir welding process parameters in similar and dissimilar alloys, such as joining of aluminum alloys16), dissimilar Al alloys17), and Mg alloys18). However, no effort is yet made to perform this optimization on FSSW of AA6061 and AZ31B dissimilar joints using RSM. This investigation is focused on the optimization of the important FSSW process parameters such as tool rotational speed, plunge rate, dwell time, and tool diameter ratio to attain the maximum strength in dissimilar joints of AA6061 aluminum and AZ31B magnesium alloys.
2. Experimental Procedure
The base materials used in this investigation are the rolled sheets of 2.45 mm thick AA6061 aluminum alloy and 3 mm thick AZ31B magnesium alloy. The chemical composition of the base materials are presented in Table 1. The mechanical properties of the base materials are presented in Table 2. Based on preliminary trials and literature8-15), the independent process parameters affecting the strength of FSSW joints were identified as tool rotational speed(N), plunge rate(R), dwell time(T) and tool diameter ratio(D). The tool diameter ratio (D) is defined as the ratio between the tool shoulder diameter to the pin diameter. Feasible limits of each process parameter were chosen in such a way that the joint should be free from visible defects. The upper limit of the each process parameter was coded as +2 and lower limit as −2. The intermediate coded values were calculated from the following relationship.
where Xi is the required coded value of a variable X; X is any value of the variable from Xmin to Xmax; Xmin is the lower limit of the variable and Xmax is the upper limit of the variable. The selected process parameters with limits are presented in Table 3.
The selected design matrix is shown in Table 4. It is a four-factor, five-level central composite rotatable design matrix (CCD) consisting of 30 sets of coded conditions and composed of 16 factorial points, 8 star points and 6 center points. The 30 experimental runs allowed the estimation of the linear, quadratic and two way interactive effects of the process parameters on tensile shear fracture load (TSFL). Tools with five different shoulder diameters (Fig. 2) were fabricated using super high speed steel (SHSS). The pin diameter and pin length were maintained at 5 mm. Tapered threaded (left hand) profile was made on the pin.
All the experiments were conducted as per conditions dictated by the design matrix with the help of an indigenously designed and developed computer numerical controlled friction stir welding machine (6 Ton capacity). The aluminum sheet was used as bottom sheet and magnesium sheet was used as top sheet in lap joint configuration (Fig. 3). The fabricated FSW welded joints are shown in Fig. 4. The cross-sectional macrographs of the FSSW joints with the minimum, intermediate and maximum TSFL are presented in Fig. 5.
3. Development of Empirical Relationship
The response (Y), thetensile shear fracture load (TSFL) of FSSW joints is, a function of tool rotational speed (N), plunge rate (R), dwell time (T) and tool diameter ratio (D) and hence, it can be expressed as
For the selected four factors and the interaction factors, the selected polynomial could be expressed as
where b0 is the average of responses and b1, b2… b4, b11, b13… b44 are the coefficients that depend on the respective main and interaction effects of parameters. DESIGNEXPERT 9.1 software was used to calculate the values of these coefficients and presented in Table 5. After determining the coefficients, the empirical relationship to predict TSFL was developed. The developed empirical relationship in the coded form, is given below
The adequacy of the developed empirical relationship was tested using the analysis of variance (ANOVA) technique with the help of DESIGNEXPERT 9.1 software. The results of the ANOVA are given in Table 6. The F-value of the developed model is 165.68, which indicates that the model is significant. There is only 0.01% chance that the F-value of a model this large could occur due to noise. Values of “Prob> F” less than 0.050 indicates that the model terms are significant. In this case, N, R, T, D, NT, RT, RD, TD, N2, R2, T2 and D2 are significant model terms. Values greater than 0.10 indicates that the model terms are not significant. The lack of fit F-value of 1.78 implies that the lack of fit is not significant relative to the pure error. The non-significant lack of fit is good. The co-efficient of determination R2 values gives the goodness of fitness of the model. For a good model, R2 valueshould be close to 1. In this model the calculated R2 value is 0.99. This implies that 99% of the experimental data confirms the compatibility with the data predicted by the developed model. The value of the adjusted R2 of 0.98 also indicates the high significance of the model. The predicted R2 value is 0.96, which shows reasonable agreement with the adjusted R2 of 0.98. Adequate precision measures the signal to noise ratio, and a ratio greater than 4 is desirable. The high value shows that this model can be used to navigate the design space. The observed values and predicted values of the responses are close to each other, which indicate an almost perfect fit of the developed empirical relationship (Table 7 & Fig. 6).
4. Optimization of FSSW process parameters
The optimization of FSSW parameters was carried out using the statistical tool of response surface methodology (RSM). It is a collection of mathematical and statistical techniques useful for developing the set of experiments, establishing an empirical relationship and indicating the interaction effect between the process parameters values graphically19). Response surface graph and contour plots play a very important role in the study of a response surface. It is clear from Fig. 7(a-f) that the TSFL increases with the increase of tool rotational speed, plunge rate, and tool diameter ratio to a certain value and then decreases. It is also observed that the initial increase of dwell time increases the TSFL to a certain value and further increase of dwell time keeps the TSFL to remain constant.
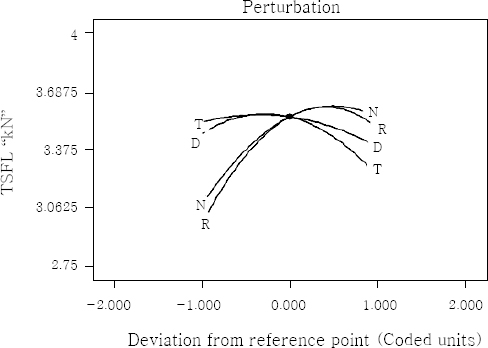
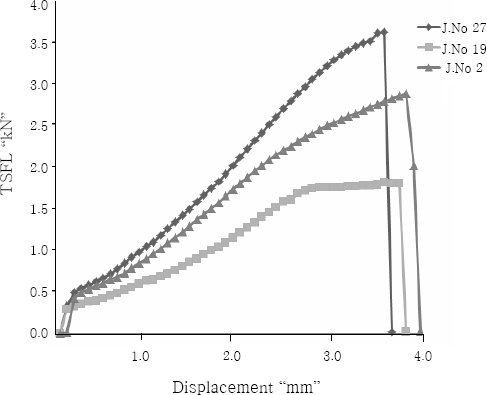
The lower tool rotational speed, high tool plunge rate, low dwell time and low tool diameter ratio (lower heat input condition) produce inadequate heat due to lower friction between the tool shoulder and weld line, which results in poor plastic flow of material in nugget and formation of defect in the nugget zone. This defect acts as a crack initiation location during shear test, and so, the TSFL is lower. The higher tool rotational speed, high dwell time, and high tool diameter ratio (higher heat condition) produce excess heat that causes metallurgical changes such as grain coarsening20), re-dissolution and coarsening of strengthening precipitates at the nugget21) and lower dislocation density that decrease the TSFL value22,23). The apex of each response graphs provides the optimal combination of parameters to attain maximum strength (TSFL). Similarly, the center of the contour plots provides the optimal combination of parameters to attain maximum strength (TSFL). Fig. 8 illustrates the perturbation plot for the response TSFL of FSSW joints. This plot provides silhouette view of the response surface and shows the change of TSFL while the parameter moves from the reference point, with all other parameters are held constant at the reference value. The perturbation plot indicates that deviation from the reference point is minimum at the maximum TSFL. It is also inferred that the TSFL varies significantly with change in tool rotational speed and plunge rate, whereas TSFL does not change significantly with variation in tool diameter ratio and dwell time. Fig. 9 shows the load displacement curves obtained during the tensile test for the typical joints.
The developed optimization procedure was validated by fabricating some more FSSW joints using optimized parameters. Table 8 summarizes the experimental values, the predicted values and the percentage of error. The validation results revealed that the developed optimization procedure is quite accurate and has good validity.
5. Conclusions
1) An empirical relationship was developed to estimate the tensile shear fracture load (strength) of friction stir spot welded dissimilar joints of AA6061 aluminum and AZ31B magnesium alloys incorporating important parameters. This relationship can be effectively used to estimate TSFL at 95% confidence level.
2) The maximum TSFL value of 3.61 kN was exhibited by the joint fabricated using a tool rotational speed of 1000rpm, plunge rate of 16 mm/min, dwell time of 5 sec and tool diameter ratio of 2.5.
3) Of the four process parameters investigated, the tool plunge rate was found to have the greatest influence on tensile shear fracture load, followed by tool rotational speed, tool diameter ratio and dwell time (as per the F ratio).