1. ņä£ ļĪĀ
ņäØņ£Ā ņŚÉļäłņ¦Ć ņ×ÉņøÉĻ│╝ ļŹöļČłņ¢┤ LNGņŚÉ ļīĆĒĢ£ ņłśņÜöĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā ņ׳ņ£╝ļ®░ ņØ┤ņŚÉ ļö░ļØ╝ LNGņäĀĻ│╝ Ēā▒Ēü¼ņØś ņłśņÜöĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ļź╝ ņĀ£ņ×æĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö Ļ░ĢļÅäņÖĆ ņÜ®ņĀæņä▒, ļé┤ņŗØņä▒ņØ┤ ņÜ░ņłśĒĢ£ Al 5083 ĒĢ®ĻĖłņ£╝ļĪ£ ņŻ╝ļĪ£ ņé¼ņÜ®ļÉśļ®░, ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖłņØś ņäĀņ▓┤ņØś ņĀ£ņ×æņŚÉ ņ׳ņ¢┤ņä£ ņÜ®ņĀæņØĆ ļ¦żņÜ░ ņżæņÜöĒĢ£ Ļ│ĄņĀĢņØ┤ ļÉ£ļŗż. ĻĘĖļ¤¼ļéś ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖłņØĆ Ļ│Āņ▓┤ļ│┤ļŗż ņĢĪņ▓┤ ņāüĒā£ņŚÉņä£ ļåÆņØĆ ņłśņåī ņÜ®ĒĢ┤ļÅäļź╝ Ļ░Ćņ¦äļŗż
1). ņØ┤ļŖö ņĢīļŻ©ļ»ĖļŖä ņÜ®ņĀæ ņŗ£ ĻĖ░Ļ│ĄņØś ņŻ╝ļÉ£ ņøÉņØĖņØ┤ ļÉ£ļŗż
2). ņØ┤ļ¤¼ĒĢ£ ņĢīļŻ©ļ»ĖļŖä ņÜ®ņĀæņØś ļŗ©ņĀÉņØä ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢśņŚ¼ Plasma-MIG (Metal Inert Gas)ņÖĆ Ļ░ÖņØĆ ļ│ĄĒĢ®ņŚ┤ņøÉņØś ņÜ®ņĀæ Ļ│ĄņĀĢņØ┤ ņłśņåīņØś ņśüĒ¢źņØä ņĄ£ņåīĒÖöĒĢĀ ņłś ņ׳ļŖö ļ░®ļ▓Ģņ£╝ļĪ£ ņĀüņÜ®ļÉĀ ņłś ņ׳ļŗż.
Ton ņØĆ
3) ļ╣äļÅÖņČĢ Plasma-MIG ņÜ®ņĀæņŚÉņä£ Ļ┤æĒĢÖ ļČäĻ┤æļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņĢäĒü¼ņØś ņś©ļÅäļČäĒżļź╝ ņĖĪņĀĢĒĢśņśĆĻ│Ā, ņÖĆņØ┤ņ¢┤ņŚÉ ņØśĒĢ┤ ĒØÉļź┤ļŖö ņĀäļźśņÖĆ ĒöīļØ╝ņ”łļ¦ł ņĀäļźśņÖĆņØś Ļ┤ĆĻ│äļź╝ ĒÖĢņØĖĒĢśņśĆļŗż. Essers ļō▒ņØĆ
4) Plasma-MIG ņÜ®ņĀæĻ│╝ MIG ņÜ®ņĀæ ņżæ ļ¬©ņ×¼ņØś ņŚ┤ļ¤ēņØä ņĖĪņĀĢĒĢśņŚ¼ ņŚ┤ņĀäļŗ¼ ļ®öņ╣┤ļŗłņ”śĻ│╝ ņÜ®ņ×ģļ®┤ņĀüņØä ļ╣äĻĄÉ ļČäņäØĒĢśņśĆļŗż. Ono ļō▒ņØĆ
5) ņĢīļŻ©ļ»ĖļŖäņØä ņÜ®ņĀæĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ĒöīļØ╝ņ”łļ¦ł ņÜ®ņĀæĻ│╝ MIG ņÜ®ņĀæ ĒåĀņ╣śļź╝ ļÅÖņČĢņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņŚ¼ ņŖżĒī©Ēä░ņÖĆ ĒØäņØś ņĀĆĻ░ÉņØä ĒÖĢņØĖĒĢśņśĆĻ│Ā, ņÖĆņØ┤ņ¢┤ ņśłņŚ┤ņØä ĒåĄĒĢ┤ ļ¦łĻĘĖļäżņŖś ĻĖ░ĒÖöĒśäņāüņØä ņżäņØ┤Ļ│Ā, ņĢłņĀĢņĀüņØĖ ņĢäĒü¼Ļ░Ć ĒśĢņä▒ļÉ©ņØä ĒÖĢņØĖĒĢśņśĆļŗż. Kim
6) Ļ│╝ Jung
7) ļō▒ņØĆ ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖł 4tņÖĆ 6tņÜ®ņĀæņØś Ļ│ĄņĀĢ ļ│Ćņłś ņśüĒ¢źļĀźņØä ļČäņäØĒĢśĻ│Ā, ĻĖ░ņĪ┤ MIG ņÜ®ņĀæĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ņāØņé░ņä▒ ņĖĪļ®┤ņŚÉņä£ ņ£Āļ”¼ĒĢśļŗżĻ│Ā ņäżļ¬ģĒĢśņśĆļŗż.
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö, ņÖĆņØ┤ņ¢┤ņÖĆ ļ¬©ņ×¼ņØś ņłśņåī ļ░Å ņłśļČä Ēś╝ņ×ģņØä ļ░®ņ¦ĆĒĢśĻ│Ā, ĻĖ░Ļ│Ą ļ░Å ĻĘĀņŚ┤ņØś ļ»╝Ļ░ÉļÅäļź╝ ļé«ņČöĻĖ░ ņ£äĒĢ┤ Plams-MIG ĒĢśņØ┤ļĖīļ”¼ļō£ ņÜ®ņĀæņØä ņØ┤ņÜ®ĒĢśņŚ¼ IĒśĢ ļ¦×ļīĆĻĖ░ ĒśĢņāüņŚÉ ļīĆĒĢ£ ņåīņ×¼ ļæÉĻ╗ś 6t ņÜ®ņĀæņØä ņ¦äĒ¢ēĒĢśņśĆļŗż. Plasma-MIG ĒĢśņØ┤ļĖīļ”¼ļō£ ņÜ®ņĀæņŚÉņä£ Ļ░ü ņÜ®ņĀæ ņØĖņ×ÉļōżņØ┤ ņÜ®ņĀæļČĆ Ļ░ĢļÅäņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źļĀźĻ│╝ ņÜ®ņĀæļČĆ ņØĖņןĻ░ĢļÅä ņśłņĖĪņØä ņ£äĒĢśņŚ¼ ĒåĄĻ│äņĀü ĒÜīĻĘĆļ¬©ļŹĖĻ│╝ ņØĖĻ│ĄņŗĀĻ▓Į ĒÜīļĪ£ļ¦ØņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņÜ®ņĀæļČĆ Ļ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ņé¼ņÜ®ļÉ£ ĒÜīĻĘĆļ¬©ļŹĖņØĆ 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖ(second order polynomial regression model), ĻĘĖļ”¼Ļ│Ā ļŗżņżæ ļ╣äņäĀĒśĢ ĒÜīĻĘĆļ¬©ļŹĖ(multiple nonlinear regression model)ņØ┤ļ®░ ĒåĄĻ│äņĀü ļ¬©ļŹĖĻ│╝ ļ╣äĻĄÉĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņØĖĻ│Ąņ¦ĆļŖź ņĢīĻ│Āļ”¼ņ”śņØä ņØ┤ņÜ®ĒĢ£ ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖ(neural network model)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. Ļ░£ļ░£ļÉ£ ļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņŗżņĀ£ Ļ░ĢļÅäņÖĆ ņśłņĖĪĻ░ÆņŚÉ ļīĆĒĢ£ ĒÅēĻĘĀ ņśżņ░©ņ£©ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ü ļ¬©ļŹĖņØś ņĀĢļ¤ēņĀüņØĖ ņśłņĖĪ ņä▒ļŖźņØä ĒÖĢņØĖĒĢśņśĆļŗż.
2. ņŗżĒŚś ņןņ╣ś ļ░Å ņÜ®ņĀæ ņĪ░Ļ▒┤
2.1 ņŗżĒŚś ņןņ╣ś ļ░Å ņÜ®ņĀæ ņ×¼ļŻī
ņŗżĒŚśņŚÉ ņé¼ņÜ®ļÉ£ ņÜ®ņĀæņןņ╣śļŖö ĒöīļØ╝ņ”łļ¦łņÖĆ MIG ņÜ®ņĀæņØ┤ ļ│ĄĒĢ®ņŚ┤ņøÉņ£╝ļĪ£ ņ×æņÜ®ĒĢśļŖö ņŗ£ņŖżĒģ£ņ£╝ļĪ£
Fig. 1Ļ│╝ Ļ░ÖņØ┤ ĒöīļØ╝ņ”łļ¦ł ļ░£ņāØ ļģĖņ”ÉĻ│╝ GMAWņØś ņÖĆņØ┤ņ¢┤Ļ░Ć ļÅÖņČĢņ£╝ļĪ£ Ļ│ĄĻĖēļÉśļŖö ņŗ£ņŖżĒģ£ņØ┤ļŗż. ņÜ®ņĀæņØĆ Plasma-MIG ņÜ®ņĀæ ĒåĀņ╣śļŖö ļĪ£ļ┤ćņŚÉ Ļ│ĀņĀĢļÉśņ¢┤ ņ׳Ļ│Ā ņÜ®ņĀæĒĢśĻ│Āņ×É ĒĢśļŖö ņŗ£ĒÄĖņØä Ļ│ĀņĀĢ ņןņ╣ś (fit-up device)ļĪ£ ņ¦ĆĻĘĖņØś ļ▓Āļō£(bed)ņŚÉ Ļ│ĀņĀĢļÉśņ¢┤ ņÜ®ņĀæ ņ¦äĒ¢ē ļ░®Ē¢źņØś ļ░śļīĆ ļ░®Ē¢źņ£╝ļĪ£ ņØ┤ņåĪĒĢśņŚ¼ ņÜ®ņĀæņØ┤ ņłśĒ¢ēļÉ£ļŗż. ņÜ®ņĀæņØś ņ×ÉļÅÖņĀüņØĖ ņŗ£ņŖżĒģ£ ņÜ┤ņśüņØä ņ£äĒĢ┤ 3ņČĢ xyz ĒģīņØ┤ļĖö ņØ┤ņåĪ ņŗ£ņŖżĒģ£ņØä ņØ┤ņÜ®ĒĢśņśĆļŗż.
Fig.┬Ā1
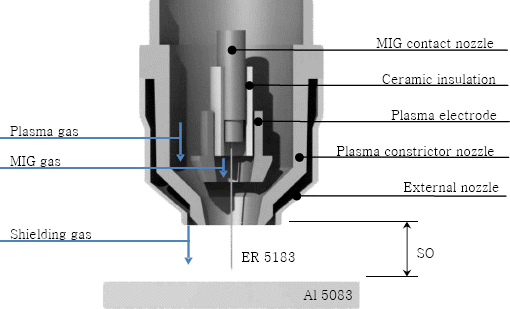
ņŗżĒŚśņŚÉ ņé¼ņÜ®ļÉ£ ļ¬©ņ×¼ļŖö Al 5083-H321 ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖłņ£╝ļĪ£ ĻĘĖ ņĪ░ņä▒ņØĆ
Table 1Ļ│╝ Ļ░Öļŗż. ņŗ£ĒÄĖņØĆ 250mm ├Ś 150mm ├Ś 6mmņØś Ēü¼ĻĖ░ļź╝ Ļ░¢Ļ│Ā ņ׳ļŗż. ņÜ®ņĀæņÖĆņØ┤ņ¢┤ļŖö 5000Ļ│äņŚ┤ ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖłņŚÉ ņŻ╝ļĪ£ ņé¼ņÜ®ļÉśļŖö ER 5183ņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņé¼ņÜ®ļÉ£ ņÜ®ņĀæ ņÖĆņØ┤ņ¢┤ņØś ņ¦üĻ▓ĮņØĆ 1.2mmņØ┤ļŗż. ER 5183ņØś ņĪ░ņä▒ņØĆ
Table 1Ļ│╝ Ļ░Öļŗż. ņÜ®ņĀæņØĆ ļ¦×ļīĆĻĖ░ ņÜ®ņĀæņ£╝ļĪ£ ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░ ņŗ£ĒÄĖņØ┤ ļ¦×ļŗ┐ļŖö ļČĆļČäņØĆ ļ░Ćļ¦üņ£╝ļĪ£ Ļ░ĆĻ│ĄĒĢśņŚ¼ ĻĘĖ ļ®┤ņØä ņØ╝ņĀĢĒĢśĻ▓ī ĒĢśņśĆļŗż. ņÜ®ņĀæņØĆ ņØ┤ņåĪ ļ▓Āļō£(bed)ņŚÉ ņØśĒĢ┤ ņŗ£ĒÄĖņØ┤ ņøĆņ¦üņØ┤ļŖö ļ░®ņŗØņ£╝ļĪ£ ņÜ®ņĀæ ĻĖĖņØ┤ļŖö 130mm ņśĆļŗż.
Table┬Ā1
Chemical composition of Al alloys (wt.%)
|
Si |
Cu |
Mn |
Mg |
Zn |
Cr |
Ti |
Al |
|
Al 5083 |
0.4 |
0.1 |
0.7 |
4.5 |
0.25 |
0.15 |
0.15 |
Bal. |
|
ER5183 |
0.4 |
0.1 |
0.75 |
4.75 |
0.15 |
0.11 |
0.15 |
Bal. |
2.2 ņÜ®ņĀæ ņŗżĒŚś Ļ│äĒÜŹ ļ░Å ņĪ░Ļ▒┤
ņØ╝ļ░śņĀüņ£╝ļĪ£ Plasma-MIG ņÜ®ņĀæņŚÉņä£ ņŻ╝ņÜö ņÜ®ņĀæ Ļ│ĄņĀĢ ļ│ĆņłśļŖö ĒöīļØ╝ņ”łļ¦ł ņÜ®ņĀæ ņØĖņ×ÉņØĖ ĒöīļØ╝ņ”łļ¦ł ņĀäļźśņÖĆ ņĀäņĢĢ ļō▒ņØ┤ ņ׳Ļ│Ā, GMAW ņÜ®ņĀæņØś ņØĖņ×ÉņØĖ ņĢäĒü¼ ņĀäļźśņÖĆ ņĀäņĢĢ, CTWD (Contact tube to workpiece distance) ļō▒ņØ┤ ņĪ┤ņ×¼ ĒĢ£ļŗż. ļ┐Éļ¦ī ņĢäļŗłļØ╝ Ļ│ĄņĀĢ ļ│ĆņłśļĪ£ņŹ©, ņÜ®ņĀæ ņåŹļÅä, Ļ░ĆņŖżņØś ņ£Āļ¤ē, Ēīüļ¬©ņ×¼Ļ░ä Ļ▒░ļ”¼ ļō▒ņØ┤ ņ׳ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ļŗżņ¢æĒĢ£ ņØĖņ×É ņżæņŚÉņä£ ņÜ®ņĀæļČĆņØś ņ×ģņŚ┤ņŚÉ ņŻ╝ņÜö ņØĖņ×ÉļĪ£ ņé¼ļŻīļÉśļŖö ĒöīļØ╝ņ”łļ¦ł ņÜ®ņĀæ ņĀäļźś(plasma welding current: PWC), MIG ņÜ®ņĀæ ņĀäņĢĢ (MIG Welding voltage: GWV), ņÖĆņØ┤ņ¢┤ ņåĪĻĖēņåŹļÅä (wire feeding rate: WFR), ņÜ®ņĀæ ņåŹļÅä (welding speed: WS)ļź╝ ņäĀĒāØĒĢśņśĆļŗż. Ļ░ü ņÜ®ņĀæ ļ│ĆņłśņŚÉ ļīĆĒĢ£ ņłśņżĆĻ│╝ ĻĘĖ Ļ░ÆņØĆ ņśłļ╣ä ņŗżĒŚśņØä ĒåĄĒĢśņŚ¼ ņäĀņĀĢĒĢśņśĆĻ│Ā ņØ┤Ļ▓āņØĆ
Table 2ņÖĆ Ļ░Öļŗż.
Table┬Ā2
Factors and levels of orthogonal experiment
|
No. |
Factor |
Level 1 |
Level 2 |
Level 3 |
|
A |
Plasma welding current: PWC(A) |
120 |
140 |
160 |
|
B |
MIG welding voltage: GWV(V) |
25 |
26 |
27 |
|
C |
Wire feed rate: WFR(m/min) |
16 |
18 |
20 |
|
D |
Welding speed: WS(mm/s) |
14 |
15 |
16 |
ļ│Ė ņÜ®ņĀæņØä ņĀäņłśļĪ£ ņłśĒ¢ēĒĢ£ļŗżļ®┤, ņ┤Ø 81ĒÜīņØś ņŗżĒŚśņØä ņłśĒ¢ēĒĢśņŚ¼ņĢ╝ ĒĢ£ļŗż. ĻĘĖļ¤¼ļéś ņŗżĒŚśņØś ĒÜ©ņ£©ņä▒ ĒÖĢļ│┤ļź╝ ņ£äĒĢśņŚ¼ ņØ╝ļČĆņŗżņŗ£ļ▓Ģ(fractional factorial design)ņżæ ĒĢśļéśņØĖ ņ¦üĻĄÉ ļ░░ņŚ┤ļ▓Ģ(orthogonal design)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņŗżĒŚśņØä ņ¦äĒ¢ēĒĢśņśĆļŗż. ņ¦üĻĄÉ ļ░░ņŚ┤Ēæ£(table of orthogonal arrays)ņŚÉ ņØśĒĢśņŚ¼ 3ņłśņżĆĻ│äņØä ņé¼ņÜ®ĒĢśņŚ¼ ĻĄ¼ņä▒ĒĢ£ ņŗżĒŚś ņĪ░Ļ▒┤ņØĆ ņ┤Ø 27Ļ░£ņØś ņĪ░Ļ▒┤ņØä ņØ┤ņÜ®ĒĢśņśĆļŗż.
Plasma-MIG ņÜ®ņĀæņØś Ļ│ĀņĀĢņØĖņ×ÉļĪ£ļŖö ĒöīļØ╝ņ”łļ¦ł ņĀäĻĘ╣Ļ│╝ ļ¬©ņ×¼Ļ░ä Ļ▒░ļ”¼(torch standoff: SO)ļŖö 10mmļĪ£ ĒĢśņśĆņ£╝ļ®░, ņÜ®ņĀæņŚÉ ĒĢäņÜöĒĢ£ Ļ░ĆņŖżļŖö ļ¬©ļæÉ 99.99% ņł£ļÅäļź╝ Ļ░¢ļŖö ņĢäļź┤Ļ│ż Ļ░ĆņŖżļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. Ļ░üĻ░üņØś Ļ░ĆņŖż Ļ│ĄĻĖē ņ£Āļ¤ēņ£╝ļĪ£ MIG Ļ░ĆņŖż, ĒöīļØ╝ņ”łļ¦ł Ļ░ĆņŖż, ņ░©ĒÅÉ Ļ░ĆņŖżļŖö 10L/min, 10L/min, 15L/minļĪ£ ņäżņĀĢĒĢśņŚ¼ Ļ│ĄĻĖēĒĢśņśĆļŗż.
3. ņÜ®ņĀæļČĆ ņØĖņןĻ░ĢļÅä
Al 5083 ĒĢ®ĻĖłņØś Plasma-MIG ņÜ®ņĀæņŚÉņä£ ņÜ®ņĀæļČĆņØś ĻĖ░Ļ│äņĀü Ļ░ĢļÅäļź╝ ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņØĖņןņŗ£ĒŚśņØä ņłśĒ¢ēĒĢśņśĆļŗż. ņØĖņן ņŗ£ĒŚśņØĆ KS B ISO 4136
8)ņØś ĻĘ£ņĀĢņŚÉ ļö░ļØ╝ ņ¦äĒ¢ēĒĢśņśĆņ£╝ļ®░ ņØĖņן ņŗ£ĒÄĖņØś ņ╣śņłśļŖö
Fig. 2ņÖĆ Ļ░Öļŗż. ĻĘĖļ”╝ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ņÜ®ņĀæļČĆņØś ņØĖņן Ļ░ĢļÅäļź╝ ņĖĪņĀĢĒĢśĻĖ░ ņ£äĒĢ┤ņä£ ņÜ®ņĀæļČĆņØś ļŹ¦ņé┤ (reinforcement)ļź╝ ņĀ£Ļ▒░ĒĢśņŚ¼ ņŗżĒŚśņØä ņłśĒ¢ēĒĢśņśĆļŗż. ļ¬©ņ×¼ņØś ņØĖņןĻ░ĢļÅäļŖö 351N/mm
2 ņØ┤Ļ│Ā Al 5083 ļ¬©ņ×¼ņØś ņĄ£ņåī ņØĖņןĻ░ĢļÅäļŖö AWS(american welding society)ņŚÉņä£ 270N/mm
2ļĪ£ ĻĘ£ņĀĢĒĢśĻ│Ā ņ׳ļŗż
9). ņÜ®ņĀæļČĆņØś ņØĖņן Ļ░ĢļÅä Ļ▓░Ļ│╝ļŖö
Table 3Ļ│╝ Ļ░Öļŗż.
Fig.┬Ā2

Table┬Ā3
|
No. |
PWC (A) |
GWV (V) |
WFR (m/min) |
WS (mm/s) |
TS (N/mm2) |
|
1 |
120 |
25 |
16 |
14 |
173.86 |
|
2 |
140 |
25 |
18 |
14 |
195.23 |
|
3 |
160 |
25 |
20 |
14 |
97.04 |
|
4 |
140 |
26 |
16 |
14 |
135.94 |
|
5 |
160 |
26 |
18 |
14 |
127.72 |
|
6 |
120 |
26 |
20 |
14 |
292.43 |
|
7 |
160 |
27 |
16 |
14 |
95.91 |
|
8 |
120 |
27 |
18 |
14 |
288.3 |
|
9 |
140 |
27 |
20 |
14 |
85.91 |
|
10 |
140 |
25 |
16 |
15 |
149.31 |
|
11 |
160 |
25 |
18 |
15 |
142.46 |
|
12 |
120 |
25 |
20 |
15 |
293.37 |
|
13 |
160 |
26 |
16 |
15 |
162.33 |
|
14 |
120 |
26 |
18 |
15 |
181.15 |
|
15 |
140 |
26 |
20 |
15 |
278.98 |
|
16 |
120 |
27 |
16 |
15 |
210.25 |
|
17 |
140 |
27 |
18 |
15 |
223.25 |
|
18 |
160 |
27 |
20 |
15 |
116.65 |
|
19 |
160 |
25 |
16 |
16 |
155.26 |
|
20 |
120 |
25 |
18 |
16 |
181.86 |
|
21 |
140 |
25 |
20 |
16 |
153.44 |
|
22 |
120 |
26 |
16 |
16 |
* |
|
23 |
140 |
26 |
18 |
16 |
142.36 |
|
24 |
160 |
26 |
20 |
16 |
183.71 |
|
25 |
140 |
27 |
16 |
16 |
108 |
|
26 |
160 |
27 |
18 |
16 |
151.81 |
|
27 |
120 |
27 |
20 |
16 |
285.18 |
Table 3ņØś 22ļ▓ł ņŗżĒŚśņØś Ļ▓ĮņÜ░ ņÜ®ņ×ģņØ┤ ņĀüņ¢┤ ņØĖņןņŗ£ĒŚśņØä ņłśĒ¢ēĒĢśņ¦Ć ļ¬╗ĒĢ£ Ļ▓░ņĖĪņ╣śņØ┤ļŗż. ņÜ®ņĀæļČĆņØś ļ╣äļō£ ĒśĢņāüņØĆ
Fig. 3Ļ│╝ Ļ░Öļŗż. Ēæ£ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ņØĖņןņŗ£ĒŚś Ļ▓░Ļ│╝ ļīĆļČĆļČä ĒöīļØ╝ņ”łļ¦ł ņĀäļźśĻ░Ć ļé«ņØĆ 120A, ņÖĆņØ┤ņ¢┤ ņåĪĻĖēņåŹļÅäĻ░Ć ļåÆņØĆ 20 m/minņŚÉņä£ ņĄ£ņåīņØĖņןĻ░ĢļÅä ļ│┤ļŗż ļåÆņØĆ Ļ▓░Ļ│╝Ļ░Ć ļéśņÖöļŗż. ņØ┤Ļ▓āņØĆ
Fig. 3ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ņÖäņĀä ņÜ®ņ×ģņØ┤ ļ░£ņāØļÉśļŖö Ļ▓ĮņÜ░ņØ┤ļ®░ ņÖäņĀä ņÜ®ņ×ģĻ│╝ ļ╣äļō£ ĒśĢņāüņØ┤ ņÜ░ņłśĒĢ£ Ļ▓ĮņÜ░ ņÜ®ņĀæ Ļ░ĢļÅäĻ░Ć ļåÆĻ▓ī ļéśĒāĆļé¼ļŗż. ĻĘĖļ¤¼ļéś ņÜ®ņĀæ ņ×ģņŚ┤ņØ┤ ņĀüņØĆ ņÜ®ņĀæ ņĀäļźśĻ░Ć ļé«Ļ│Ā, ņÜ®ņĀæ ņåŹļÅäĻ░Ć ļ╣ĀļźĖ Ļ▓ĮņÜ░ļŖö
Fig. 3ņØś
(a)ņÖĆ Ļ░ÖņØ┤ ļČłņÖäņĀä ņÜ®ņ×ģņØ┤ ļ░£ņāØĒĢśņśĆņ£╝ļ®░, ņØ┤ņŚÉ ļö░ļØ╝ ņØĖņן Ļ░ĢļÅäĻ░Ć ļé«ņĢśļŗż. ļ░śļ®┤ ĒöīļØ╝ņ”łļ¦łņØś ņĀäļźśĻ░Ć ļåÆĻ│Ā, ņÜ®ņĀæ ņåŹļÅäĻ░Ć ļŖÉļ”░ Ļ▓ĮņÜ░ņŚÉ ņ׳ņ¢┤ņä£ļŖö
Fig. 3ņØś
(c)ņÖĆ Ļ░ÖņØ┤ ņÜ®ļØĮĒśäņāüņØ┤ ļ░£ņāØĒĢśņŚ¼ ņÜ®ņĀæļČĆņØś Ļ░ĢļÅäļź╝ ņĀĆĒĢśņŗ£ĒéżļŖö ņøÉņØĖņ£╝ļĪ£ ņ×æņÜ®ĒĢ£ļŗż.
Fig.┬Ā3

4. Ļ│ĄņĀĢļ│Ćņłśļź╝ ņØ┤ņÜ®ĒĢ£ ņØĖņןĻ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖ
Ļ│ĄņĀĢļ│Ćņłśļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ņÜ®ņĀæņä▒ņØä ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢ£ ļ░®ļ▓Ģ ņżæ ĒĢśļéśļĪ£ ņØĖņןĻ░ĢļÅäļź╝ ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä ņĀ£ņŗ£ĒĢśĻ│Āņ×É ĒĢ£ļŗż. ņŗżĒŚś ņĪ░Ļ▒┤ļé┤ņŚÉņä£ ņÜ®ņĀæ Ļ│ĄņĀĢļ│ĆņłśņŚÉ ļīĆĒĢśņŚ¼ Al 5083 ņĢīļŻ©ļ»ĖļŖä ĒĢ®ĻĖłņØś ņĄ£ņåīņØĖņןĻ░ĢļÅäļ│┤ļŗż ļåÆņØĆ ņØĖņןĻ░ĢļÅäņØä Ļ░¢ļŖö ņĪ░Ļ▒┤ņØä ņśłņĖĪĒĢśņŚ¼ ņŗ£ņŖżĒģ£ņØä ļ¬©ļŹĖļ¦ü ĒĢśĻ▓ī ļÉśļ®┤, ņŗżĒŚś ĻĄ¼Ļ░äļé┤ņŚÉņä£ ņŗżĒŚśĒĢśņ¦Ć ļ¬╗ĒĢ£ ņ×ģļĀź ņĪ░Ļ▒┤ņŚÉ ļīĆĒĢśņŚ¼ ņČ£ļĀźņØä ĻĘ╝ņé¼ņĀüņ£╝ļĪ£ ĻĄ¼ĒĢĀ ņłś ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĒåĄĻ│äņĀüņØĖ ņĀæĻĘ╝ ļ░®ņŗØņØś ĒÜīĻĘĆļ¬©ļŹĖ(regression model)Ļ│╝, ĒĢÖņŖĄņŚÉ ņØśĒĢ£ ņØĖĻ│Ąņ¦ĆļŖźĒśĢ ņŗĀĻ▓Įļ¦Øļ¬©ļŹĖ(neural network model)ņØä ņĀ£ņŗ£ĒĢśņśĆļŗż.
4.1 ĒÜīĻĘĆ ļČäņäØņØä ņØ┤ņÜ®ĒĢ£ ņØĖņןĻ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖ
ĒÜīĻĘĆļČäņäØ(regression analysis)ņØ┤ļ×Ć ļ│Ćņłśļōż Ļ░äņØś Ļ┤ĆļĀ©ņä▒ņØä ĻĘ£ļ¬ģĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņ¢┤ļ¢ż ņłśĒĢÖņĀü ļ¬©ĒśĢņØä Ļ░ĆņĀĢĒĢśĻ│Ā, ņØ┤ ļ¬©ĒśĢņØä ņĖĪņĀĢļÉ£ ļ│ĆņłśļōżņØś ļŹ░ņØ┤Ēä░ļĪ£ļČĆĒä░ ņČöņĀĢĒĢśļŖö ĒåĄĻ│äņĀü ļČäņäØ ļ░®ļ▓ĢņØä ļ¦ÉĒĢ£ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņÜ®ņĀæņØś ņ×ģņŚ┤ ņØĖņ×Éļź╝ ņ×ģļĀź ļ│ĆņłśļĪ£, ļ░śņØæļ│ĆņłśļĪ£ļŖö ņÜ®ņĀæļČĆņØś ņÜ®ņĀæņä▒ņØä ļéśĒāĆļé╝ ņłś ņ׳ļŖö ņØĖņןĻ░ĢļÅäļĪ£ ĒĢśņŚ¼ ļ¬©ļŹĖļ¦üĒĢśņśĆļŗż.
ņØĖņן Ļ░ĢļÅäņśłņĖĪņØä ņ£äĒĢ┤ņä£ ņé¼ņÜ®ļÉ£ ļ¬©ļŹĖņØĆ Ēü¼Ļ▓ī 2Ļ░Ćņ¦Ćļź╝ ņØ┤ņÜ®ĒĢśņśĆļŗż. 3ņןņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ņÜ®ņĀæļČĆņØś Ļ░ĢļÅäļŖö ņÜ®ņĀæ ĒśĢņāüĻ│╝ Ļ┤ĆļĀ©ļÉśņ¢┤ ļ¦żņÜ░ ļ╣äņäĀĒśĢņĀüņØĖ ļ¬©ņŖĄņØä Ļ░¢Ļ▓ī ļÉ£ļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ņØ┤ļź╝ ļ░śņśüĒĢśņŚ¼ 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖ(second order polynomial regression model: Model I)Ļ│╝ ļŗżņżæ ļ╣äņäĀĒśĢ ĒÜīĻĘĆļ¬©ļŹĖ(multiple nonlinear regression model: Model II)ņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. Ļ░ü ļ¬©ļŹĖņØĆ ņŗØ (1)Ļ│╝ (2)ņÖĆ Ļ░Öļŗż.
ņ£äņØś ņŗØņŚÉņä£ x1, x2, x3, x4 ļŖö ņÜ®ņĀæ ņ×ģļĀźļ│ĆņłśļĪ£ņä£ ņł£ņä£ļīĆļĪ£ ĒöīļØ╝ņ”łļ¦ł ņÜ®ņĀæ ņĀäļźś, MIG ņÜ®ņĀæ ņĀäņĢĢ, ņÖĆņØ┤ņ¢┤ ņåĪĻĖēņåŹļÅä ĻĘĖļ”¼Ļ│Ā ņÜ®ņĀæņåŹļÅäņØ┤ļŗż. Ļ░ü ņ×ģļĀźļ│ĆņłśņØś Ļ░ÆņØĆ 0ņŚÉņä£ 1ņØś Ļ░Æņ£╝ļĪ£ Ēæ£ņżĆĒÖö (normalization)ņØä ĒĢ£ Ļ░ÆņØä ņé¼ņÜ®ĒĢśņśĆļŗż. y╠éļŖö ņóģņåŹļ│ĆņłśļĪ£ Ļ░ü ļ¬©ļŹĖņŚÉ ņØśĒĢ┤ ņśłņĖĪļÉśņ¢┤ņ¦ä ņØĖņןĻ░ĢļÅä Ļ░ÆņØ┤ļŗż. ļśÉĒĢ£ ╬▓0ļŖö ĒÜīĻĘĆ ļ¬©ļŹĖņØś ņĀłĒÄĖņØ┤Ļ│Ā, ╬▓i, ╬▓ij ļŖö ļÅģļ”Įļ│ĆņłśņØś Ļ│äņłśĻ░ÆņØä ļéśĒāĆļéĖļŗż. Ļ░üĻ░üņØś Ļ│äņłś
ļŖö ņĄ£ņåīņĀ£Ļ│▒ļ▓Ģ(method of least squares)ņ£╝ļĪ£ ņČöņĀĢĒĢ£ļŗż. Ļ░ü ļ¬©ļŹĖņØś Ļ│äņłśļŖö
Table 3Ļ│╝
4ņÖĆ Ļ░Öļŗż.
Table┬Ā4
Coefficients for regression model I
|
╬▓0
|
╬▓1
|
╬▓2
|
╬▓3
|
╬▓4
|
|
182 |
-97.7 |
150 |
45.1 |
13.7 |
|
╬▓11
|
╬▓12
|
╬▓13
|
╬▓14
|
╬▓22
|
|
62.4 |
-153 |
-76.7 |
131 |
-45.4 |
|
╬▓23
|
╬▓24
|
╬▓33
|
╬▓34
|
╬▓44
|
|
-30.1 |
86.9 |
-16.6 |
55 |
-128 |
Table┬Ā5
Coefficients for regression model II
|
╬▓0
|
╬▓1
|
╬▓2
|
╬▓3
|
╬▓4
|
|
201 |
-145 |
61.6 |
6.7 |
17.5 |
ĒÜīĻĘĆ ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ¢╗ņ¢┤ņ¦ä ņÜ®ņĀæļČĆņØś ņØĖņןĻ░ĢļÅä ņśłņĖĪ Ļ▓░Ļ│╝ļŖö
Fig. 4ņÖĆ
5ņÖĆ Ļ░Öļŗż. ĻĘĖļ”╝ņŚÉņä£ Ļ░ĆļĪ£ ņČĢņØĆ ņśłņĖĪļÉ£ ņØĖņןĻ░ĢļÅäļź╝ ņäĖļĪ£ ņČĢņØĆ ņŗżņĀ£ ņŗżĒŚśņŚÉņä£ ņ¢╗ņ¢┤ņ¦ä ņØĖņןĻ░ĢļÅä ņØ┤ļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ĻĘĖļלĒöäļé┤ņØś ņ¦üņäĀņŚÉ Ļ░ĆĻ╣īņÜĖņłśļĪØ ņśłņĖĪ ņä▒ļŖźņØ┤ ņÜ░ņłśĒĢśļ®░, ņĀĢņä▒ņĀüņ£╝ļĪ£ ĒÖĢņØĖĒĢĀ ļĢī 2ņ░© ļŗżĒĢŁĒÜīĻĘĆ ļ¬©ļŹĖņØ┤ ņóĆ ļŹö ņśłņĖĪņØä ņלĒĢśĻ│Ā ņ׳ņØīņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā4
Estimation results of model I(second order polynomial regression model)

Fig.┬Ā5
Estimation results of model II (multiple nonlinear regression model)

4.2 ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ņśłņĖĪ ļ¬©ļŹĖ
ņÜ®ņĀæļČĆņØś ņØĖņןĻ░ĢļÅäļź╝ ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ┤ņä£ ņØĖĻ│Ąņ¦ĆļŖźĒśĢ ņĢīĻ│Āļ”¼ņ”śņØś ĒĢśļéśņØĖ ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ņÜ®ņĀæ Ļ│ĄņĀĢļ│ĆņłśņŚÉ ļīĆĒĢ£ ņØĖņןĻ░ĢļÅäņØś ņśłņĖĪņØ┤ ļ╣äņäĀĒśĢņØ┤ Ļ░ĢĒĢśļ»ĆļĪ£ ņØ┤ļź╝ ņל ļ░śņśüĒĢĀ ņłś ņ׳ļŖö ņŗĀĻ▓Įļ¦Ø ļ¬©ļŹĖņØä ļśÉ ļŗżļźĖ ņśłņĖĪļ¬©ļŹĖļĪ£ ņäĀņĀĢĒĢśņśĆļŗż. ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØĆ ĒĢÖņŖĄĒĢśļŖö ļŖźļĀźņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ņ£╝ļ»ĆļĪ£ ņÜ®ņĀæĻ│ĄņĀĢĻ│╝ Ļ░ÖņØ┤ ņłśĒĢÖņĀüņ£╝ļĪ£ ļ¬©ļŹĖļ¦üĒĢśĻĖ░ ņ¢┤ļĀżņÜ┤ ļ╣äņäĀĒśĢņĀü ņÜöņåīļź╝ ļ¦ÄņØ┤ ĒżĒĢ©ĒĢ£ ļČäņĢ╝ņŚÉ ļīĆĒĢśņŚ¼ Ļ┤æļ▓öņ£äĒĢśĻ▓ī ņĀüņÜ®ļÉśĻ│Ā ņ׳ļŗż
10,11).
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņé¼ņÜ®ļÉśļŖö ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖ (Model III)ņØĆ
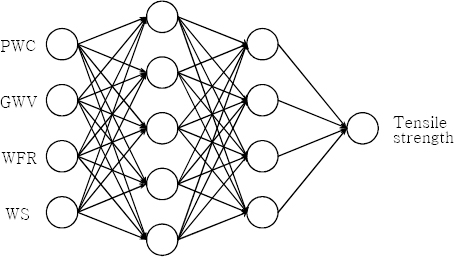
Fig. 6Ļ│╝ Ļ░Öļŗż. ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ĻĄ¼ņĪ░(architecture)ļź╝ ņ¢╗ĻĖ░ ņ£äĒĢśņŚ¼ ņäĀĒŚśņĀü(heuristic)ņ£╝ļĪ£ 1Ļ░£ņØś ņ×ģļĀźņĖĄ(input layer)Ļ│╝ 2Ļ░£ņØś ņØĆļŗēņĖĄ(hidden layer) ĻĘĖļ”¼Ļ│Ā ņČ£ļĀźņĖĄ(output layer)ņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņŚ¼ ļ¬ć Ļ░Ćņ¦Ć ĻĄ¼ņĪ░ņØś ņĪ░ĒĢ®ņŚÉ ļīĆĒĢśņŚ¼ ņśżļ▓äĒö╝Ēīģ(overfitting)ņØ┤ ļÉśņ¦Ć ņĢŖļÅäļĪØ ņØĆļŗēņĖĄņØś ļģĖļō£ņØś Ļ░£ņłśļź╝ ļŗżņ¢æĒĢśĻ▓ī ĒĢÖņŖĄņØä ņłśĒ¢ēĒĢśņśĆĻ│Ā, ņĄ£ņåīņØś ļģĖļō£ļź╝ ņØ┤ņÜ®ĒĢśļÅäļĪØ ĒĢÖņŖĄņä▒ņØä ĒģīņŖżĒŖĖ ĒĢ£ Ēøä
Fig. 6Ļ│╝ Ļ░ÖņØĆ ļ¬©ļŹĖņØä ņäĀņĀĢĒĢśņśĆļŗż.
Fig.┬Ā6
Neural network model architecture
Ļ░ü ļģĖļō£ņØś ņŚ░Ļ▓░ Ļ░ĢļÅäļź╝ ĒĢÖņŖĄņŗ£ĒéżĻĖ░ ņ£äĒĢ£ ņĢīĻ│Āļ”¼ņ”śņ£╝ļĪ£ ņśżļźś ņŚŁņĀäĒīī(error backpropagation) ņĢīĻ│Āļ”¼ņ”śņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ĒĢÖņŖĄņ£©(learning rate)ņØĆ 0.1 ņØ┤Ļ│Ā, ņ¦ĆņŚŁņĀü ņĄ£ņåīņĀÉ(local minimum)ļ¼ĖņĀ£ņÖĆ ļ╣ĀļźĖ ņłśļĀ┤ņ£╝ļĪ£ ĒĢÖņŖĄ ņåŹļÅäļź╝ ņ£äĒĢ┤ ļ¬©ļ®śĒģĆ ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśņśĆņ£╝ļ®░, ļ¬©ļ®śĒģĆ Ļ│äņłś(momentum coefficient)ļŖö 0.9ļĪ£ ņäżņĀĢĒĢśņśĆļŗż. Ļ░ü ļĀłņØ┤ņ¢┤ņØś ņĀäļŗ¼ĒĢ©ņłś(transfer function)ļŖö ņ×ģļĀźņĖĄĻ│╝ 1ņ░© ņØĆļŗēņĖĄ ņé¼ņØ┤ņŚÉļŖö ĒāäņĀĀĒŖĖ ņŗ£ĻĘĖļ¬©ņØ┤ļō£(tan-sigmoid) ņĀäļŗ¼ĒĢ©ņłśļź╝ 1ņ░©ņÖĆ 2ņ░© ņØĆļŗēņĖĄ Ļ░äĻ│╝ 2ņ░© ņØĆļŗēņĖĄĻ│╝ ņČ£ļĀźņĖĄ Ļ░äņØś ņĀäļŗ¼ĒĢ©ņłśļŖö 1ņ░© ņäĀĒśĢ(purelin) ņĀäļŗ¼ĒĢ©ņłśļź╝ ņé¼ņÜ®ĒĢśņśĆļŗż.
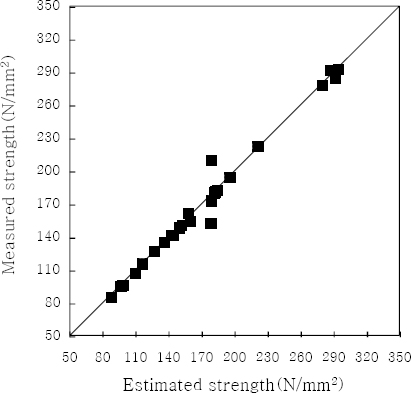
Fig. 7ņØĆ ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØś ņśłņĖĪ Ļ▓░Ļ│╝ņØ┤ļŗż. ĻĘĖļ”╝ņŚÉņä£ ļ│┤ļŖö ļ░öņÖĆ Ļ░ÖņØ┤ ĒÜīĻĘĆļ¬©ļŹĖņØś ņśłņĖĪ ļ│┤ļŗżļŖö ņ¦üņäĀņŚÉ Ļ░ĆĻ╣īņÜ┤ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ņØ┤Ļ▓āņØĆ ļ╣äņäĀĒśĢņä▒ņØ┤ Ēü░ ņÜ®ņĀæņŚÉņä£ļŖö ĒĢÖņŖĄņØś ĒÜ©Ļ│╝ņÖĆ ļ╣äņäĀĒśĢņØä ņל Ēæ£ĒśäĒĢ┤ ņżä ņłś ņ׳ļŖö ņØĖĻ│ĄņŗĀĻ▓ĮĒÜīļĪ£ļ¦ØņØś ļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØ┤ ņÜ░ņłśĒĢ©ņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
Fig.┬Ā7
Estimation results of model III(neural network model)
4.3 ņśłņĖĪļ¬©ļŹĖņØś ņä▒ļŖź ļ╣äĻĄÉ
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö Plasma-MIG ņÜ®ņĀæņØä ņĀüņÜ®ĒĢ£ ņĢīļŻ©ļ»ĖļŖä Al 5083 ĒĢ®ĻĖłņØś ņÜ®ņĀæļČĆ ņØĖņןĻ░ĢļÅäļź╝ ņśłņĖĪĒĢśļŖö ļ¬©ļŹĖņØä ņĀ£ņĢłĒĢśņśĆļŗż. ņĀ£ņĢłļÉ£ ļ¬©ļŹĖņØĆ ņ┤Ø 3Ļ░£ļĪ£ņä£ 2Ļ░£ņØś ĒÜīĻĘĆļ¬©ļŹĖĻ│╝ 1Ļ░£ņØś ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØ┤ļŗż. ņØ┤ļ¤¼ĒĢ£ ļ¬©ļŹĖņØś ņśłņĖĪ ņä▒ļŖźņØä ņĀĢļ¤ēņĀüņ£╝ļĪ£ ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ĒÅēĻĘĀ ņśżņ░©ņ£©(average error rate: AER)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ░ü ņśłņĖĪ ļ¬©ļŹĖņØä ļ╣äĻĄÉĒĢśņśĆļŗż. ĒÅēĻĘĀņśżņ░©ņ£©ņØś ņŗØņØĆ ņŗØ (3)Ļ│╝ Ļ░Öļŗż.
ņŚ¼ĻĖ░ņä£ iļŖö ņŗżĒŚś ļ▓łĒśĖņØ┤Ļ│Ā, nņØĆ ņ┤Ø ņŗżĒŚś ĒܤņłśļĪ£ 26ņØ┤ļŗż. yļŖö ņĖĪņĀĢļÉ£ ņØĖņןĻ░ĢļÅäņØ┤ļ®░, y╠éļŖö ņśłņĖĪļ¬©ļŹĖņŚÉ ņØśĒĢ┤ ņśłņĖĪļÉ£ Ļ░ÆņØ┤ļŗż.
Ļ░ü ņśłņĖĪņä▒ļŖźņØä ļ╣äĻĄÉĒĢ£ Ļ▓░Ļ│╝ļŖö
Table 6Ļ│╝ Ļ░Öļŗż. 2Ļ░£ņØś ĒÜīĻĘĆ ļ¬©ļŹĖ ņżæņŚÉņä£ļŖö 2ņ░© ļŗżĒĢŁĒÜīĻĘĆļ¬©ļŹĖņØś ĒÅēĻĘĀņśżņ░©ņ£©ņØ┤ 0.125ļĪ£ ļåÆņĢśņ¦Ćļ¦ī, ņĀäņ▓┤ 3Ļ░£ņØś ļ¬©ļŹĖ ņżæņŚÉņä£ļŖö ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØ┤ 0.021ļĪ£ ņØĖņןĻ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖ ņżæ Ļ░Ćņן ņÜ░ņłśĒĢ£ ļ¬©ļŹĖņ×äņØä ņĢī ņłś ņ׳ņŚłļŗż.
Table┬Ā6
Average error rate comparison for each model
|
Model |
I |
II |
III |
|
AER |
0.125 |
0.238 |
0.021 |
5. Ļ▓░ ļĪĀ
ļ│Ė ņŚ░ĻĄ¼ļŖö ņĢīļŻ©ļ»ĖļŖä Al 5083 6t ĒĢ®ĻĖłņŚÉ ļīĆĒĢ£ Plasma-MIG ņÜ®ņĀæņØä ņŗżĒŚśĻ│äĒÜŹļ▓ĢņŚÉ ļö░ļØ╝ ņłśĒ¢ēĒĢśņśĆņ£╝ļ®░, ņÜ®ņĀæļČĆņØś ņØĖņןĻ░ĢļÅäļź╝ ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż. ņÜöņĢĮļÉ£ ļģ╝ļ¼ĖņØś Ļ▓░ļĪĀņØĆ ņĢäļלņÖĆ Ļ░Öļŗż.
1) Al 5083 6t ĒĢ®ĻĖłņØś Plasma-MIG ņÜ®ņĀæņŚÉņä£ ņÜ®ņĀæ Ļ│ĄņĀĢļ│ĆņłśņØĖ ĒöīļØ╝ņ”łļ¦ł ņĀäļźś, MIG ņÜ®ņĀæ ņĀäņĢĢ, ņÖĆņØ┤ņ¢┤ ņåĪĻĖēņåŹļÅä, ņÜ®ņĀæņåŹļÅäņŚÉ ļö░ļźĖ ņÜ®ņĀæ ĒŖ╣ņä▒ņØä ņÜ®ņĀæļČĆ ņØĖņן ņŗ£ĒŚśņØä ĒåĄĒĢśņŚ¼ ĒīīņĢģĒĢśņśĆļŗż. ņÜ®ņĀæļČĆļŖö ņ×ģņŚ┤ņŚÉ ļö░ļźĖ ņÜ®ņ×ģĒŖ╣ņä▒ņŚÉ ļö░ļØ╝ Ļ░ĢļÅä ļ│ĆĒÖöļź╝ ĒÖĢņØĖĒĢĀ ņłś ņ׳ņŚłļŗż.
2) ņÜ®ņĀæļČĆņØś Ļ░ĢļÅäņŚÉ ļīĆĒĢ£ ņśłņĖĪ ļ¬©ļŹĖņØä 2ņ░© ļŗżĒĢŁ ĒÜīĻĘĆļ¬©ļŹĖ, ĻĘĖļ”¼Ļ│Ā ļŗżņżæ ļ╣äņäĀĒśĢ ĒÜīĻĘĆļ¬©ļŹĖ, ĻĘĖļ”¼Ļ│Ā ņØĖĻ│Ąņ¦ĆļŖź ņĢīĻ│Āļ”¼ņ”śņØä ņØ┤ņÜ®ĒĢ£ ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ 3Ļ░£ņØś Ļ░ĢļÅä ņśłņĖĪ ļ¬©ļŹĖņØä Ļ░£ļ░£ĒĢśņśĆļŗż.
3) Ļ░ü ļ¬©ļŹĖņØś ņĀĢļ¤ēņĀü ņśłņĖĪ ņä▒ļŖźņØä ĒÅēĻĘĀ ņśżņ░©ņ£©ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļ╣äĻĄÉĒĢśņśĆĻ│Ā, ņĀäņ▓┤ 3Ļ░£ņØś ļ¬©ļŹĖ ņżæņŚÉņä£ļŖö ĒĢÖņŖĄņØś ĒÜ©Ļ│╝ņÖĆ ļ╣äņäĀĒśĢņØä ņל Ēæ£ĒśäĒĢ┤ ņżä ņłś ņ׳ļŖö ņŗĀĻ▓ĮĒÜīļĪ£ļ¦Ø ļ¬©ļŹĖņØś ĒÅēĻĘĀ ņśżņ░©ņ£©ņØ┤ 0.021ļĪ£ Ļ░Ćņן ņÜ░ņłśĒĢ£ ļ¬©ļŹĖņ×äņØä ĒÖĢņØĖĒĢśņśĆļŗż.
Ēøä ĻĖ░
ņØ┤ ļģ╝ļ¼ĖņØĆ ļČĆĻ▓ĮļīĆĒĢÖĻĄÉ ņ×Éņ£©ņ░ĮņØśĒĢÖņłĀ ņŚ░ĻĄ¼ļ╣ä(2014ļģä)ņŚÉ ņØśĒĢśņŚ¼ ņŚ░ĻĄ¼ļÉśņŚłņØī










 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print