Fatigue Analysis of the Effects of Incomplete Penetration Defects on Fatigue Crack Initiation Points in Butt-Welded Members
Article information
Abstract
Fatigue life evaluation of steel structures is a very important issue in their design and maintenance. For steel structure maintenance, it is particularly important to know when and where fatigue cracks are initiated in aging steel bridges. To calculate the fatigue life and identify crack initiation points in butt-welded members, a fatigue finite element method was developed in this study. First, to represent weld fatigue phenomena, this study applied the finite displacement theory and elastic-plastic cycle hysteresis constitutive model to reproduce large deformations and repeated load phenomena. Then, the damage mechanics theory was applied to reproduce fatigue cracks and assess the fatigue life. The effect of incomplete penetration defects on fatigue life and crack initiation points of butt-welded members were clarified using fatigue finite element method. Results also showed that crack initiation points and fatigue life were different depending on the depth of incomplete penetration. The FEM results were considered reliable after comparing with results from Hotspot stresses, IIW and DNV-GL.
1. Introduction
The number of aging steel structures, such as aging bridges, that must be maintained are gradually increasing. As a result, the need to perform safety inspections is also increasing. On the other hand, in carrying out safety inspections of aging bridges, many incomplete penetration defects are found in the weld joints. However, it is difficult to judge to what depth the penetration defect extends, so a fatigue assessment method is needed to evaluate whether incomplete penetration defects are safe or not. These welded butt members with incomplete penetration have weld toe and incomplete penetration depth. Also, butt welded joints have portions where stress is concentrated not only from welding but also from repeated loading. Therefore, it is difficult to ascertain the fatigue crack initiation point from experimental research. In this study, three-dimension fatigue FEM was proposed and used to determine fatigue life and crack initiation.
The theory of continuum damage mechanics is employed in fatigue FEM and cyclic hysteresis fatigue models, which are demonstrated by the cyclic hysteresis constitutive equation and continuum damage theory. Also, characteristics of several fatigue phenomena were formulated to apply fatigue FEM. The formulated typical theories are combined the isotropic hardening rule and kinematic hardening rule, ratcheting effect, and strain range effect and mean stress effect and damage theory etc35-37,46).
Among the various factors that affect fatigue life and crack initiation, this study focuses on the effect of incomplete penetration depth. It is difficult to find the fatigue crack initiation point by experiment because it is prone to various experimental errors and it is hard to know the crack initiation point in cases where it occurs internally. There are several studies related to welding defects of butt members. These studies dealt mainly with stress concentration and fatigue life by experiment12-14,31-34).
2. FE welding analysis procedure for butt-welded member
Since cracks mainly occur in the weld joints, the welded member should be reproduced. Also, residual stresses are thought to influence fatigue strength1-3). The initial residual welding stresses and welding deformations were analyzed to reproduce the initial mechanical state of the butt-welded member. The welding residual stresses and deformation values were calculated by using a 3D non-steady heat conduction FEA and a 3D thermal elastio-plastic FEA. The welding temperature history obtained by non-steady heat conduction analysis was used as initial data for the welding residual stress and welding deformation analysis. These welding analysis methods have been extensively verified4-7). The welding analysis procedure based on an in-house program consists of two steps for reproducing the butt-welded member7). In the first step, a 3D non-steady heat conduction analysis was performed to find the welding temperature hysteresis. In the second step, a 3D large deformation thermal elastic-plastic analysis was performed to obtain the welding residual stress and welding deformation.
2.1 FE welding analysis model
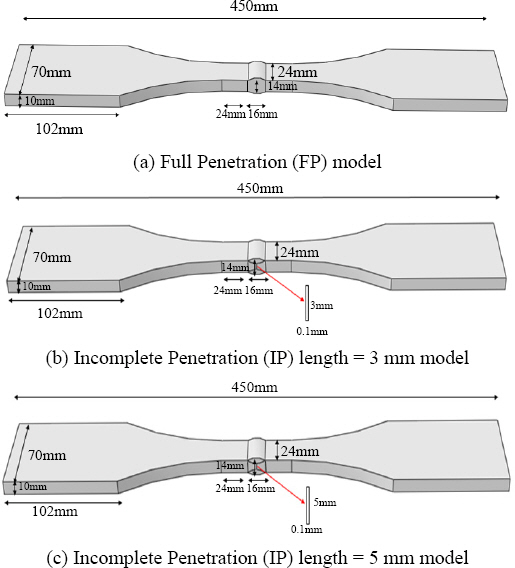
Butt-welded members were investigated to clarify the effect of incomplete penetration depth on fatigue crack initiation point and fatigue life. The dimensions and general view of the butt members are shown in Fig. 1. The case of full penetration (FP) model and incomplete penetration (IP) model had penetration depths of 3 mm and 5 mm, respectively .SM490 steels were used as the base metal in analysis. The mesh size of the butt member is shown in Fig. 2. The 3D finite element mesh type with eight-node isoparametric solid elements was used. A fine mesh was used at the weld because the cracks occur near the weld. Also, because the mesh size affects results, the spacing between fine meshes used was 2 mm, a value which is obtained empirically. A coarse mesh was used away from the weld. The properties of temperature-dependent thermo-physical such as specific heat, heat conductivity and density of the material were employed in the non-steady heat conduction analysis.
2.2 Welding temperature and thermal elastic-plastic analysis results
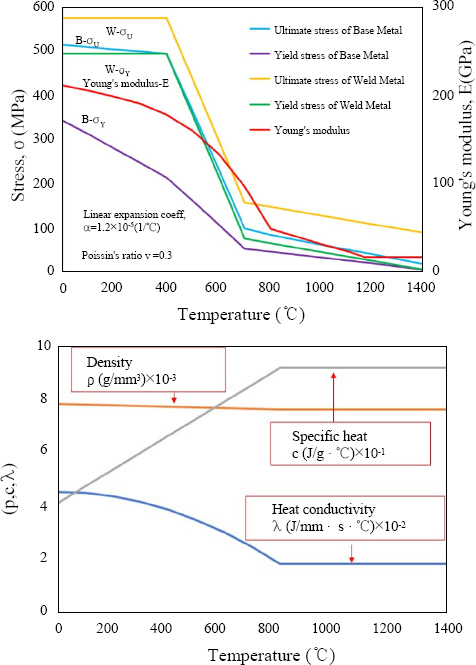
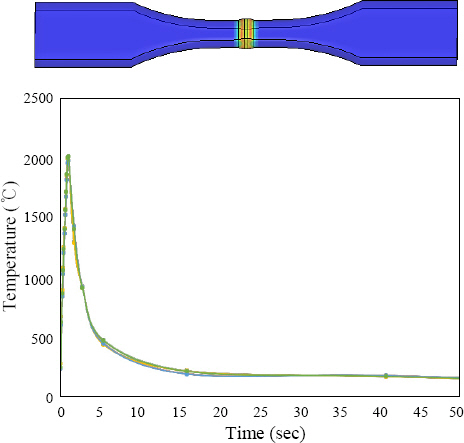
The mechanical properties and physical constants change according to the temperature change under welding. Thus, the properties of material are defined by temperature-dependent thermo-physical and mechanical properties such as yield stress, ultimate stress and Young’s modulus of the base member and weld metals. Fig. 3 shows the properties of the material. Fig. 4 shows a result of the temperature distribution calculated from the non-steady heat conduction analysis. The boundary conditions used during welding analysis is shown by Fig. 5. To find the residual stresses and welding deformations, the temperature history was introduced in the 3D thermal elasto-plastic FEA as the initial thermal load6,7). Fig. 6(a), (b), and (c) show the residual stresses of butt-welded members at the upper parts. The result of residual stresses of full penetration is shown Fig. 6(a). The results of partial penetration model are shown Figs. 6(b) and (c). The welding deformations were analyzed by using a 3D large deformation thermal elasto-plastic FEA. Fig. 7(a), (b) and (c) show a sample of welding displacements of nodal points at the upper surface. The results indicate that there was little difference in displacements as the model size was small, so in order to visualize these differences in figures we have multiplied the data by 5. The displacement in Fig. 7(a) is small compared to Fig. 7(b) and Fig. (c) as the residual stresses in full penetrated butt welded member was small compared to incomplete penetrated butt welded members (3mm and 5mm).whereas the displacement in Incomplete penetration butt welded members were same as the residual stress in z direction was almost same.
3. Fatigue test for butt-welded members
The fatigue test was performed by using an MTS809- 250KN servo-hydraulic testing machine to verify the analysis results of the fatigue FEM. A standard-size specimen was used for the fatigue experiment. The fatigue FEM analysis was performed with identically sized test specimen. The welding condition was full penetration welding. The load was applied by displacement control. The fatigue testing method for the welded specimen was carried out based on the ASTM standard. Dimensions of butt-welded specimens, geometry, and MTS machine for testing are shown in Fig. 8. The fatigue test results are shown in Fig. 11. The results of analysis and experimental are in good agreement and satisfy the S-N curves of IIW.
4. Fatigue FE analysis for butt-welded members
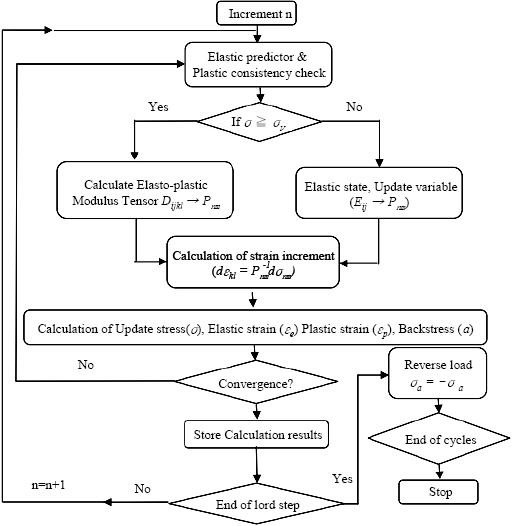
In fatigue analysis, CDM20-27) was considered46). Fig. 9 shows the overall numerical procedures. The other formulated procedures have been extensively published in other papers35-37).
4.1 Load and boundary conditions of fatigue FEA
Fig. 10(a) shows the load type applied. A repeated load was given by the displacement control. The magnitude of varying displacement amplitude was given from 0.3 to 0.6mm. The applied load is different depending on the stress range. The minimum value is 0.0 mm. The boundary conditions are shown in Fig. 10(b). The one end of the member was fixed in the all directions. The loads were equally distributed to the other end of the member.
4.2 Effect of incomplete penetration depth on fatigue life
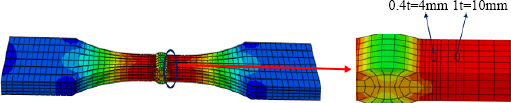
The effect of incomplete penetration depth on fatigue life and fatigue crack initiation was investigated. Fig. 11 shows the results of fatigue life for FP and IP model. It was found that the fatigue strength and life of incomplete penetration member is lowered than that of full penetration member. The analysis results (■■■) were compared with the results (▲) of experiment. Also, the results were compared with the results of hot spot stress method (◆◆◆) that was frequently used structural design field. Fig. 12 shows the models used for the calculation of HSS. The results of fatigue FEA with the butt member was compared with the results of the HSS method shown in Fig. 11. The HSS method with the fine mesh model from IIW was used in the calculation. Fig. 12 shows model for HSS and surface stress extrapolation at the weld toe recommended by IIW. The formula for the surface stress extrapolation is given as σhs = 1.67σ0.4t - 0.67σ1.0t . The number of cycles was obtained as follows: N = C x (1/Ks)-m x (σhs)-m , where Ks = 1.24, C = 1.1 x 1013 , and m = 3.51.
There was no difference in the fatigue life regardless of whether the penetration is incomplete. As expression of fatigue life loaded by uniaxial force are used by the S-N curve from the fatigue experiment. The S-N curve is generally indicated by a relationship of the stress range and the fatigue life. Because the results of fatigue FEM analysis are in a three-dimension multiaxial stress state, the longitudinal axis of the S-N curve was expressed by applying the equivalent stress range, which can denote the multiaxial stress state in order to compare with the existing S-N curve. The fatigue life was decided by the number of cycles when the first crack occurred at model. On the other hand, in the hot-spot stress (HSS) method mainly used in the design field, the left axis is expressed as an HSS range instead of a stress range. The S-N curves of fatigue analysis were compared with the S-N curve of IIW18) and DNV10). All values of S-N curve are satisfied the S-N curves of IIW and DNV.
4.3 Effect of incomplete penetration depth on crack initiation point
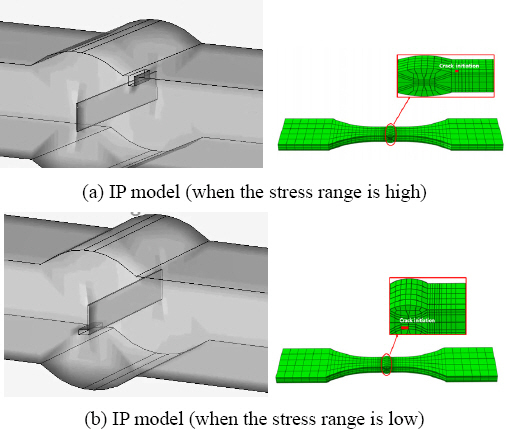
The effect of incomplete penetration depth on crack initiation point was investigated for butt members. Crack initiation point of full penetration model is shown in Fig. 13. Initial crack occurred in the end part of the weld line when the stress range is high. On the other hand, initial crack occurred at the middle part of weld line when the stress range is low.
And, the effect of incomplete penetration depth was investigated, for that case the penetration depth is 3mm and 5mm, respectively. In the case of 3mm, the results are shown in the Fig. 14. Initial crack occurred in the end part of the weld line when the stress range is high. On the other hand, Initial crack occurred at the end part of the penetration depth when the stress range is low. In the case of 5mm, the results are shown in the Fig. 15. Initial crack occurred at the end part of the penetration depth regardless of stress range is high or low. As a result, it was found that incomplete penetration depth and stress range has a significant influence on the crack initiation point.
5. Conclusion
The 3D fatigue analysis method was proposed based on continuum damage mechanics to investigate the effect of incomplete penetration defects on fatigue life and fatigue crack initiation point. In addition, 3D non-steady heat conduction analysis and thermal elastic-plastic analysis were performed to reproduce the initial butt-welded member. The following conclusions are summarized from this study.
1) The fatigue life of butt-welded members results obtained by fatigue FEM, the HSS method, and experiments were compared.
2) The fatigue life was different depending on the depth of incomplete penetration. The S-N curves of butt members with incomplete penetration obtained by using fatigue FEM satisfied the S-N curves recommended by IIW and DNV.
3) Using fatigue FEM clarified the effect of incomplete penetration defects on fatigue life and crack initiation point.
4) The effect of incomplete penetration defects on fatigue life and crack initiation point by using fatigue FEM was investigated for butt-welded members. It was found that the initiation point of crack was different depending on the depth of incomplete penetration.
5) In the case of full penetration in the butt joint, initial cracks occurred at the end of the weld line when the stress range was high, and initial cracks occurred in the middle of the weld line when the stress range was low.
6) In the case where the IP depth is 3 mm, initial cracks occurred at the end of weld line when the stress range was high, and initial cracks occurred at the penetration depth when the stress range was low.
7) In the case where the IP depth is 5 mm, initial cracks occurred at the penetration depth regardless of the stress range.
8) Fatigue FEM is useful for calculating fatigue life and finding the crack initiation point.
Acknowledgments
This Research was supported by Chung-Ang University research grants in 2018 and by the Basic Science Resear- ch Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2016R1D1A1B04930897).